“AI can detect signs of Alzheimer”, “AI can see who is gay”, “AI predicts next recession”. We are getting used to seeing claims that "an AI" can do all sorts of things. And it becomes quite credible, given the amazing stuff we can now download to our phones.
One of the more controversial applications of "AI" is a system apparently already in use in the United States for estimating the likelihood that convicted criminals will reoffend in the future. The whole concept has been criticized for being racist, and because the private enterprise that provides the algorithm doesn't disclose it.
But the implicit assumption, even among many critics, seems to be that if you let a computer do something, it will automatically be fair. Everyone is treated the same. You take away all emotions, prestige, bias, and prejudice, and base the decision on facts and logic only.
A claim that can be found here and in several other articles is that the algorithm has been shown to consistently be much more likely to false-flag black people as high risk of recidivism, and conversely more often mistakenly classify white people as low risk.
An article in Pro Publica then goes on to say that:
"If computers could accurately predict which defendants were likely to commit new crimes, the criminal justice system could be fairer and more selective about who is incarcerated and for how long. The trick, of course, is to make sure the computer gets it right."
No it isn't.
As far as I can see there is no evidence that there is anything wrong with the algorithm. The problem is that the idea of determining time in jail based on statistical predictions of risk of reoffending is incompatible with individual justice, and enforces structural racism.
Let's first straighten one thing out: Even though the AI probably doesn't have direct information about ethnicity or skin color, this correlates with a number of factors like education, employment, living standards and so on. Therefore even if we don't tell the computer who is black and who is white, its output may still correlate strongly with it. So we might as well assume that the AI (indirectly, but still) has information about people's ethnicity and how it correlates with crime.
But even if black people are convicted more often on average than white people, shouldn't the mistakes of the algorithm go equally often in both directions? Isn't the apparent bias an indication that something is wrong with the algorithm?
No. This is the problem. And it has to do with a simple mathematical fact that won't go away no matter how you tinker with the algorithm.
Suppose instead, just to take a less controversial and more clear-cut example, that you would try to predict the outcomes of games in some sports event like a soccer league. You can see from statistics that team A seems to be the strongest, winning more than 50% of its games no matter the opposition, and conversely that team Z loses a majority of their games even against the weaker of the other teams.
Then your best bet isn’t going to be some scenario where team A wins 70% of the games, or whatever their statistics is. Instead you maximize your expected number of correct predictions by guessing that team A will win every single game, and similarly that team Z will be losing all the time.
This guess, which is the best one given the information you have, will appear unfair if you look at the cases where it was incorrect. It will happen much more often that team Z is incorrectly predicted to lose, and that team A is incorrectly predicted to win, than the other way around. Because in this example the other way around never happens, as team A is always predicted to win, and team Z always predicted to lose.
The same thing will probably happen (to some extent, but less clear-cut) if we try to guess whether people will commit crimes based on for instance their level of education and where they live (things which incidentally also correlate with ethnicity).
And there is no way of making this go away by fixing a bug in the algorithm, because it doesn't have anything to do with the computer or the code. If you try to predict criminality based on a factor X that correlates with it, then people who have X will more often be labeled high-risk, and also more often be false-flagged as high-risk.
Letting such predictions influence penalties is simply incompatible with individual justice.
There is much more to be said about this, for instance regarding the fact that there is a strong political movement in Sweden and in many other countries that would like to have precisely this form of structural discrimination and that actually prefers that to individual justice, as long as they get to choose which factors to incorporate (like being an immigrant) and which factors to ignore (like membership in the Nordic Resistance Movement).
Monday, September 25, 2017
Monday, July 31, 2017
Besserwisserpoker
Besserwisserpoker är ett kortspel som jag hittade på efter en diskussion på Olle Häggströms blogg för snart fem år sedan, och som jag nämnde igen för några dagar sedan då jag var hos mina vänner Lori och Fredrik. I deras sällskap kommer samtalet lätt in på matematik, spel, sannolikheter, betting, poker, och överhuvudtaget hur man tänker för att fatta rationella beslut.
Men det började med att Bo "bosjo" Sjögren frågade Olle hur man kan bedöma vem som är bäst på att tippa stryktips av två personer som, i stället för att bara välja 1, X eller 2 på varje match, får sätta procentsatser på de tre utfallen. Diskussionen kom att involvera logaritmer, entropi, begreppet ärlighet, Avogadros tal, och McCutcheonvarianten (en spelöppning i schack som verkar omges av en sorts kult). Den lär även ha renderat mig en nominering till Svenska Besserwisserföreningens hangaroundavdelning, men det är oklart om jag blev invald.
Nåväl, idén är att om till exempel person A ger utfallen 1, X och 2 sannolikheterna 55%, 20%, 25%, medan B säger 40%, 25%, 35%, och det sedan slutar med att hemmalaget vinner (alltså en etta), tyder detta på att A var lite bättre än B, i och med att A angav högre sannolikhet (55%) än B gjorde (40%) för det som faktiskt hände. Hade i stället bortalaget vunnit, skulle vi ha haft viss anledning att tro att B var bättre på att tippa.
Men om vi skulle låta A och B ange procenttal i 13 matcher och helt sonika addera de tal som tilldelats matchernas faktiska utfall, skulle det löna sig, för den som vill framstå som duktig på att tippa, att sätta 100% på det utfall man betraktar som mest sannolikt. Vi kunde då lika gärna ha låtit A och B tippa varsin rad på vanligt sätt.
Olles svar var att i stället addera logaritmerna av procenttalen. Ett värdigt besserwissersvar (notera att epitetet besserwisser har positiv klang i Olles värld), men hur motiverar man detta utan att gräva ner sig i analys och sannolikhetsteori?
En kommentator vid namn Norpan föreslog vad som ser ut att vara ekvivalent, nämligen att multiplicera procenttalen och låta produkten bli respektive tippares poängtal. Att addera logaritmer är ju enligt räknelagarna detsamma som att först multiplicera talen och sedan logaritmera, så man borde kunna jämföra tipparskickligheten hos A och B genom att jämföra produkterna av deras procenttal.
Med Norpans förslag räcker det med mellanstadiematematik, men kruxet är att om man försöker maximera väntevärdet av sin poäng, lönar det sig fortfarande att sätta 100% på det man tror mest på, trots att detta oftast ger noll poäng i slutändan! Problemet gick till slut att lösa utan logaritmer, men det jag tänkte prata om här är ett kortspel som modellerar situationen. Jag kallar det för Besserwisserpoker, och den som vill veta varför får titta på Olles blogg.
Spelet går ut på att gissa vilken av tre pokerhänder som blir starkast. De två spelarna A och B startar med ett rejält antal marker, minst tio tusen var. Kanske hundra tusen är bättre, för de kommer att försvinna snabbt! Man får ha något slags växlingssystem.
I varje runda blandar man en vanlig kortlek och delar ut tre händer med två kort vardera som i pokervarianten Texas Holdem, samt en "flopp" bestående av tre gemensamma kort. Baserat på dessa kort (som båda spelarna ser) fördelar varje spelare sina marker mellan de tre händerna. Dessa satsningar görs "simultant" i den meningen att varje spelare måste bestämma sin fördelning av marker utan att se hur motståndaren gör.
Därefter (och spelarna får nu se hur motståndaren satsade) delar man ut ytterligare två gemensamma kort. I poker kallas dessa traditionellt turn och river. Styrkan hos var och en av de tre händerna bestäms nu, precis som i Texas Holdem, av den bästa pokerhand som går att åstadkomma genom att välja ut fem av de sju tillgängliga korten (de två på respektive hand samt de fem gemensamma).
När det har konstaterats vilken eller vilka av de tre händerna som är starkast, får spelarna tillbaka de marker som satsades på dessa händer. Vinnaren är den som efter 13 omgångar har flest marker kvar, eller som i ett tidigare skede har marker kvar när motståndarens marker har tagit slut.
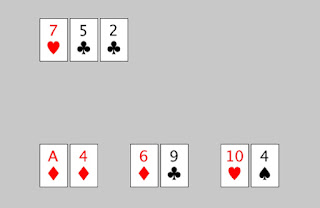
När man har delat ut en giv, kan det till exempel se ut så här:
Ingen hand har något par, så hand 1 är för tillfället starkast i kraft av sitt ess. Det kan i förstone verka som om händerna 2 och 3 är ungefär lika starka. Men hand 2 har förutom möjligheten till ett par också stegdrag, och litet färgdrag, alltså möjlighet till stege om det kommer en åtta, eller färg om det kommer två klövrar. Hand 3 å andra sidan är dominerad av hand 1 i den meningen att om det kommer en fyra, är hand 1 fortfarande bättre, och får hand 3 stege, så får hand 1 också stege.
Kontentan blir att hand 2 är nästan lika bra som hand 1, medan hand 3 ligger betydligt sämre till. Det finns $43\cdot 42 / 2 = 903$ möjligheter för de sista två gemensamma korten, och ett litet datorprogram räknar ut att hand 1 vinner ensam 444 gånger (mindre än hälften!), hand 2 vinner ensam 353 gånger, och hand 3 vinner ensam bara 84 gånger. 22 gånger får man pengarna tillbaka på både hand 1 och hand 3.
Hur ska man då satsa? Det kan vara frestande att fördela sina marker mellan enbart händerna 1 och 2. Om någon av dessa vinner, har det lönat sig att inte slösa bort något på hand 3. Men om motståndaren satsar några få marker på hand 3, blir problemet att den fördel man får när hand 1 eller 2 vinner blir mycket mindre än vad man förlorar om hand 3 skulle råka vinna.
Om man spelade ett enormt stort antal händer (och startade med ett bortom astronomiskt antal marker), skulle de optimala satsningarna behöva vara väldigt nära proportionella mot händernas sannolikheter att vinna (med vissa justeringar för möjligheten att flera händer vinner). Men när bara några få givar återstår, kommer det in spelteoretiska aspekter.
För att göra spelet skarpare kan man bestämma att en viss spelare, till exempel A, har vunnit om spelarna har lika många marker kvar på slutet (eller får slut på marker samtidigt). Denna fördel kan balanseras genom att B får starta med något fler marker.
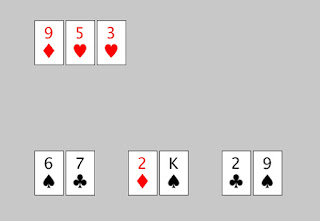
Låt oss säga att det ser ut så här på sista given, och spelarna har en mark var kvar:
Om man tillät oavgjort skulle avslutningen bli ganska slätstruken: Hand 3 har par i nior och kommer att vinna mer än hälften av gångerna. Om jag satsar min mark på hand 3, gör du bäst i att satsa på samma sätt. Den som avviker hamnar alltid i underläge. Men om A kommer att deklareras vinnare vid lika antal marker blir det mer spännande. Spelare B måste då försöka hitta på något annat. Om A satsar på hand 3 medan B väljer att satsa på hand 1 (som får stege både på en åtta och en fyra!), kommer B att vinna mer än var tredje gång.
Fast det är inte så enkelt heller. Om A anar att B tänker satsa på hand 1, kan A korsa B:s planer genom att också satsa på hand 1! Fast B kan förstås då vara en riktig lurifax och i stället själv satsa på hand 3!
Så hur ska man då spela? Svaret är att de optimala strategierna är randomiserade. För att inte bli lurad ska du i princip ha en personlig och hemlig slumptalsgenerator som i viss mån styr ditt spel. I det här fallet vinner den första handen 323 gånger och den tredje handen 487 gånger, av 903. Hand 2 vinner 93 gånger, vilket är för lite för att det ska vara rätt att någonsin satsa på den. Med bara två alternativ är regeln att spelare A, som har fördel, ska göra fel på hand 1 och hand 3 lika ofta åt båda hållen, medan spelare B som är underdog ska gissa rätt lika ofta på hand 1 som på hand 3. A ska alltså betta på hand 1 med sannolikhet $323/(323+487)$ och på hand 3 med sannolikhet $487/(323+487)$, och för B blir det tvärtom. Spelare B vinner med sannolikhet \[\frac{323\cdot 487}{(323+487) \cdot 903},\] eller ungefär 21.5%, och A alltså med sannolikhet 78.5%.
Mer komplicerat blir det om spelarna har flera marker kvar och alla tre händerna är aktuella att satsa på. Men det får räcka med spelteori för den här gången!
Men det började med att Bo "bosjo" Sjögren frågade Olle hur man kan bedöma vem som är bäst på att tippa stryktips av två personer som, i stället för att bara välja 1, X eller 2 på varje match, får sätta procentsatser på de tre utfallen. Diskussionen kom att involvera logaritmer, entropi, begreppet ärlighet, Avogadros tal, och McCutcheonvarianten (en spelöppning i schack som verkar omges av en sorts kult). Den lär även ha renderat mig en nominering till Svenska Besserwisserföreningens hangaroundavdelning, men det är oklart om jag blev invald.
Nåväl, idén är att om till exempel person A ger utfallen 1, X och 2 sannolikheterna 55%, 20%, 25%, medan B säger 40%, 25%, 35%, och det sedan slutar med att hemmalaget vinner (alltså en etta), tyder detta på att A var lite bättre än B, i och med att A angav högre sannolikhet (55%) än B gjorde (40%) för det som faktiskt hände. Hade i stället bortalaget vunnit, skulle vi ha haft viss anledning att tro att B var bättre på att tippa.
Men om vi skulle låta A och B ange procenttal i 13 matcher och helt sonika addera de tal som tilldelats matchernas faktiska utfall, skulle det löna sig, för den som vill framstå som duktig på att tippa, att sätta 100% på det utfall man betraktar som mest sannolikt. Vi kunde då lika gärna ha låtit A och B tippa varsin rad på vanligt sätt.
Olles svar var att i stället addera logaritmerna av procenttalen. Ett värdigt besserwissersvar (notera att epitetet besserwisser har positiv klang i Olles värld), men hur motiverar man detta utan att gräva ner sig i analys och sannolikhetsteori?
En kommentator vid namn Norpan föreslog vad som ser ut att vara ekvivalent, nämligen att multiplicera procenttalen och låta produkten bli respektive tippares poängtal. Att addera logaritmer är ju enligt räknelagarna detsamma som att först multiplicera talen och sedan logaritmera, så man borde kunna jämföra tipparskickligheten hos A och B genom att jämföra produkterna av deras procenttal.
Med Norpans förslag räcker det med mellanstadiematematik, men kruxet är att om man försöker maximera väntevärdet av sin poäng, lönar det sig fortfarande att sätta 100% på det man tror mest på, trots att detta oftast ger noll poäng i slutändan! Problemet gick till slut att lösa utan logaritmer, men det jag tänkte prata om här är ett kortspel som modellerar situationen. Jag kallar det för Besserwisserpoker, och den som vill veta varför får titta på Olles blogg.
Spelet går ut på att gissa vilken av tre pokerhänder som blir starkast. De två spelarna A och B startar med ett rejält antal marker, minst tio tusen var. Kanske hundra tusen är bättre, för de kommer att försvinna snabbt! Man får ha något slags växlingssystem.
I varje runda blandar man en vanlig kortlek och delar ut tre händer med två kort vardera som i pokervarianten Texas Holdem, samt en "flopp" bestående av tre gemensamma kort. Baserat på dessa kort (som båda spelarna ser) fördelar varje spelare sina marker mellan de tre händerna. Dessa satsningar görs "simultant" i den meningen att varje spelare måste bestämma sin fördelning av marker utan att se hur motståndaren gör.
Därefter (och spelarna får nu se hur motståndaren satsade) delar man ut ytterligare två gemensamma kort. I poker kallas dessa traditionellt turn och river. Styrkan hos var och en av de tre händerna bestäms nu, precis som i Texas Holdem, av den bästa pokerhand som går att åstadkomma genom att välja ut fem av de sju tillgängliga korten (de två på respektive hand samt de fem gemensamma).
När det har konstaterats vilken eller vilka av de tre händerna som är starkast, får spelarna tillbaka de marker som satsades på dessa händer. Vinnaren är den som efter 13 omgångar har flest marker kvar, eller som i ett tidigare skede har marker kvar när motståndarens marker har tagit slut.
När man har delat ut en giv, kan det till exempel se ut så här:
Ingen hand har något par, så hand 1 är för tillfället starkast i kraft av sitt ess. Det kan i förstone verka som om händerna 2 och 3 är ungefär lika starka. Men hand 2 har förutom möjligheten till ett par också stegdrag, och litet färgdrag, alltså möjlighet till stege om det kommer en åtta, eller färg om det kommer två klövrar. Hand 3 å andra sidan är dominerad av hand 1 i den meningen att om det kommer en fyra, är hand 1 fortfarande bättre, och får hand 3 stege, så får hand 1 också stege.
Kontentan blir att hand 2 är nästan lika bra som hand 1, medan hand 3 ligger betydligt sämre till. Det finns $43\cdot 42 / 2 = 903$ möjligheter för de sista två gemensamma korten, och ett litet datorprogram räknar ut att hand 1 vinner ensam 444 gånger (mindre än hälften!), hand 2 vinner ensam 353 gånger, och hand 3 vinner ensam bara 84 gånger. 22 gånger får man pengarna tillbaka på både hand 1 och hand 3.
Hur ska man då satsa? Det kan vara frestande att fördela sina marker mellan enbart händerna 1 och 2. Om någon av dessa vinner, har det lönat sig att inte slösa bort något på hand 3. Men om motståndaren satsar några få marker på hand 3, blir problemet att den fördel man får när hand 1 eller 2 vinner blir mycket mindre än vad man förlorar om hand 3 skulle råka vinna.
Om man spelade ett enormt stort antal händer (och startade med ett bortom astronomiskt antal marker), skulle de optimala satsningarna behöva vara väldigt nära proportionella mot händernas sannolikheter att vinna (med vissa justeringar för möjligheten att flera händer vinner). Men när bara några få givar återstår, kommer det in spelteoretiska aspekter.
För att göra spelet skarpare kan man bestämma att en viss spelare, till exempel A, har vunnit om spelarna har lika många marker kvar på slutet (eller får slut på marker samtidigt). Denna fördel kan balanseras genom att B får starta med något fler marker.
Låt oss säga att det ser ut så här på sista given, och spelarna har en mark var kvar:
Om man tillät oavgjort skulle avslutningen bli ganska slätstruken: Hand 3 har par i nior och kommer att vinna mer än hälften av gångerna. Om jag satsar min mark på hand 3, gör du bäst i att satsa på samma sätt. Den som avviker hamnar alltid i underläge. Men om A kommer att deklareras vinnare vid lika antal marker blir det mer spännande. Spelare B måste då försöka hitta på något annat. Om A satsar på hand 3 medan B väljer att satsa på hand 1 (som får stege både på en åtta och en fyra!), kommer B att vinna mer än var tredje gång.
Fast det är inte så enkelt heller. Om A anar att B tänker satsa på hand 1, kan A korsa B:s planer genom att också satsa på hand 1! Fast B kan förstås då vara en riktig lurifax och i stället själv satsa på hand 3!
Så hur ska man då spela? Svaret är att de optimala strategierna är randomiserade. För att inte bli lurad ska du i princip ha en personlig och hemlig slumptalsgenerator som i viss mån styr ditt spel. I det här fallet vinner den första handen 323 gånger och den tredje handen 487 gånger, av 903. Hand 2 vinner 93 gånger, vilket är för lite för att det ska vara rätt att någonsin satsa på den. Med bara två alternativ är regeln att spelare A, som har fördel, ska göra fel på hand 1 och hand 3 lika ofta åt båda hållen, medan spelare B som är underdog ska gissa rätt lika ofta på hand 1 som på hand 3. A ska alltså betta på hand 1 med sannolikhet $323/(323+487)$ och på hand 3 med sannolikhet $487/(323+487)$, och för B blir det tvärtom. Spelare B vinner med sannolikhet \[\frac{323\cdot 487}{(323+487) \cdot 903},\] eller ungefär 21.5%, och A alltså med sannolikhet 78.5%.
Mer komplicerat blir det om spelarna har flera marker kvar och alla tre händerna är aktuella att satsa på. Men det får räcka med spelteori för den här gången!
Thursday, June 29, 2017
Yatzy!
Svensk sommar är inte bara jordgubbar, mygg och bondbränna. Regniga dagar i sommarstugan hör det också till att man spelar Yatzy. Och ljusa grillkvällar kan man köra trädgårdsvarianten!
Det viktigaste är förstås att man har roligt när man spelar. Och extra roligt blir det ju när man vinner!
Ett parti yatzy handlar i hög grad om tur med tärningarna, men man kan definitivt hjälpa till själv genom de beslut man tar. Något som kanske förvånar den som mest har kört på känn är att en bra strategi kan snitta nästan 250 poäng! Eller 248.44 för att vara mer exakt. Jag skulle tro att de flesta du möter spelar bort 20 poäng eller mer per parti på beslut som inte är optimala, så om du spelar smart kan du få betydligt mer än din beskärda andel av vinster!
Här följer några tips på hur du kan tänka när du spelar. De förutsätter att du kan reglerna och har spelat ett par gånger. Tipsen bygger på vad jag själv har noterat i data från en algoritm av Jakub Pawlewicz som jag implementerade för "skandinavisk" yatzy för några år sedan. Jag plockade nyligen fram programmet igen efter att ha diskuterat yatzy med vännen Patrik Höglund, som experimenterar med att lära neurala nät spela. Tack Patte!
Mina rekommendationer skiljer sig från gängse strategi för amerikansk yatzy, vilket förklaras av skillnader i reglerna. Till exempel har vi två extra kategorier (Ett Par och Två Par), högre bonus, och räknar prickar på kåk i stället för att ha ett fast poängtal. Det här gör att det blir både lättare och viktigare för oss att få bonus, och att vi överlag fokuserar mer på femmor och sexor.
1. Säkra bonusen!
Ska du vinna i yatzy så ska du se till att få de 50 bonuspoängen, så är det bara. Vad du bör tänka på är att det är mycket viktigare att få många femmor och sexor än att få många ettor. Om du till exempel får 6-4-2-1-1 i första slaget, så spara sexan, inte ettorna! Detta har också att göra med att kombinera chanserna: Sparar du sexan kan du få en annan bra kombination, till exempel ett högt tvåpar eller en bra kåk.
Ett tidigt fyrtal i femmor eller sexor gör att du kan chansa friare i fortsättningen (se punkt 6). Se till att ta det ovanför strecket, inte på Fyrtal!
2. Håll koll på hur du ligger till för bonus!
Gränsen för bonus ligger vid 63 poäng, vilket är vad du får med tre av varje på fälten Ettor till Sexor. Du kan därför enkelt hålla koll på läget genom att jämföra med det. Om du till exempel får 20 på femmor, innebär det att du ligger +5. Skulle du sedan nöja dig med 1 poäng på Ettor, ligger du fortfarande +3, och så vidare. En tumregel är att aldrig hamna på minus med detta räknesätt. Det går förstås inte att garantera, men med en bra strategi ska du sällan riskera att missa bonusen.
3. Kombinera chanserna!
Du behöver inte bestämma dig för att försöka få en viss sak och samla till det. Spara hellre bra tärningar och se vad det blir. Om du till exempel får 6-5-2-2-1 i allra första slaget, så spara 6-5! Då kan du nästa gång bestämma om du ska satsa på femmor, sexor eller både-och.
Det är sällan man ska spara mot en straight. Undantaget är om du får 5-4-3-2. Då lönar det sig ofta att försöka sig på en straight eftersom du har chansen till både Stor och Liten. Dock är det bra om du i så fall har någon idé om vad du ska göra de nästan hälften av gångerna då detta misslyckas (se till exempel punkt 5 och 6!).
4. Spara inte på småkrafs!
Som redan har antytts bör du oftast inte spara låga par såvida du inte behöver en viss siffra för bonusen. I skandinavisk yatzy är det bara Yatzy som ger något annat än summan av de ingående tärningarna. Stegarna har förstås en fast poäng, men det du fyller i på Ett Par, Tvåpar, Tretal, Fyrtal, Kåk och Chans bör domineras av fyror, femmor och sexor. En kombination som 6-6-1-1 hör hemma på Ett Par eller Ettor, inte på Tvåpar. Mot slutet av partiet kan du dock få nöja dig med att överhuvudtaget få poäng, i synnerhet på Kåk och Fyrtal.
5. Chans är ingen slaskhög!
Använd inte Chans bara som en utväg när du inte får någon bra kombination! Fältet Chans bör helst ge minst 21 poäng. Sitter du med bara skräp efter tredje kastet är det oftast bättre att till exempel stryka Liten Straight.
Å andra sidan ska du inte vara rädd för att "slösa bort" Chans tidigt om du får bra poäng. Får du 6-6-5-4-3 tidigt, så tag Chansen! Ett Par kommer du att få igen.
6. Ettor kan vara en bra slaskhög!
Om du ligger bra till för bonus, till exempel för att du tidigt har fått 24 poäng på Sexor, kan du med fördel använda fältet Ettor som "fallskärm" efter misslyckade försök att få svårare kombinationer. Ettor kan i sig ge max 5 poäng, så om inte bonusen är i fara är det i regel bättre att stryka Ettor än att till exempel ta futtiga 17 poäng på Chans. Det här är anledningen till att du kan chansa friare om du tidigt säkrar bonusen.
7. Stryk smart!
Att behöva stryka är förstås inte roligt, men det är bara i riktigt festliga fall du kan få hela protokollet ifyllt. För det mesta kommer du att missa några kategorier, men det gör dina motståndare också. Du kan tjäna viktiga poäng genom att stryka i tid!
Om bonusen är säkrad kan du ibland offra Ettor, men i annat fall kan du behöva stryka ett svårare fält när du hade kunnat få poäng på ett lättare. Nöj dig inte med 12 poäng på Tvåpar om du i stället kan stryka Liten Straight!
Jag har ett vagt minne av att jag en gång behövde förklara för mina kära släktingar att jag inte alls var sur och att jag visst ville fortsätta spela, efter att jag hade strukit Liten Straight i första omgången!
Men Pawlewicz' algoritm ger mig upprättelse: Blir du sittande med till exempel 6-4-3-3-1 efter första omgången och säger "Äsch, 6 poäng på treor!" så har du valt det sjätte bästa alternativet. Att stryka Liten Straight är bäst. Därefter kommer att ta 1 poäng på Ettor, att stryka Stor Straight, att ta 17 på Chans, samt att ta 6 på Ett Par.
8. Var inte rädd för att stryka Yatzy!
Det bär emot att behöva stryka Yatzy. Det är liksom att ge upp spelets idé, det hörs ju på namnet. Och tänk bara nesan att sedan få Yatzy och så har man redan strukit det!
Att stryka Yatzy är dock inte som att offra kungen i schack. Du kan vinna ändå, till och med över en motståndare som har fått Yatzy. 50 poäng känns mycket, men det är faktiskt inte så ovanligt att det äts upp av övriga poäng. Nu låter det som om jag säger tvärtemot vad jag sa nyss om bonusen, men skillnaden är att du inte kan spara ihop till en Yatzy. Du kan inte öka Yatzychanserna särskilt mycket genom att offra annat.
Chansen att få Yatzy på en omgång (tre kast) är ungefär 4.6%. Även om du bara satsade på Yatzy genom hela spelet, skulle chansen att lyckas nätt och jämnt komma över 50%.
9. Överblick: Siffror, Lätta, Svåra, och Yatzy.
Ett sätt att överblicka de femton fälten på spelplanen är att gruppera dem i Siffror, Lätta, Svåra, och Yatzy. Sifferfälten är Ettor till Sexor. Därefter har vi fyra lätta fält: Ett Par, Tvåpar, Tretal och Chans (även om Chans står längre ner i protokollet). Dessa fält kommer du nästan alltid att få poäng på. Sedan kommer fyra svåra fält: Fyrtal, Liten och Stor Straight, och Kåk. Här kommer du oftast att behöva göra någon eller ett par strykningar. Slutligen har vi det svåraste fältet av alla, Yatzy!
Om du tänker så, kan du hålla reda på vilka fält du har kvar och ungefär hur du ligger till. Ett sätt att grovt hålla koll på spelarnas chanser är att utgå från att alla får bonus och att alla får poäng på de lätta fälten. Sedan blir de svåra fälten mer utslagsgivande. I väldigt runda slängar är det 20 poäng per svårt fält. Och förstås 50 för Yatzy.
10. Ta ut målvakten? Två svåra kompenserar Yatzy!
Som vi har varit inne på kan det vara dumt att ha Yatzy kvar till sist eftersom du blir utan poäng 19 gånger av 20. Å andra sidan kanske du behöver 50 poäng för att komma ikapp den som leder. Att spara Yatzy till sist är lite som att ta ut målvakten. Det ger chansen att vända ett underläge, men oftast lyckas det inte.
Om du ligger bra till kan det vara bättre att stryka Yatzy tidigare (inte för tidigt dock, yatzyrutan är värd betydligt mer tidigare i spelet!). Men om någon annan redan har fått Yatzy, ger jag då inte i praktiken upp mina chanser att vinna? Här kan en tumregel vara att du har rimliga chanser att slå en motspelare som har fått yatzy om du klarar två svåra fält mer. Det räcker inte riktigt i sig, men oftast är det så att den som har fler strykningar också har sämre poäng på de lätta fälten.
Äsch. nu blev det precis tio punkter. Vad fånigt!
Det viktigaste är förstås att man har roligt när man spelar. Och extra roligt blir det ju när man vinner!
Ett parti yatzy handlar i hög grad om tur med tärningarna, men man kan definitivt hjälpa till själv genom de beslut man tar. Något som kanske förvånar den som mest har kört på känn är att en bra strategi kan snitta nästan 250 poäng! Eller 248.44 för att vara mer exakt. Jag skulle tro att de flesta du möter spelar bort 20 poäng eller mer per parti på beslut som inte är optimala, så om du spelar smart kan du få betydligt mer än din beskärda andel av vinster!
Här följer några tips på hur du kan tänka när du spelar. De förutsätter att du kan reglerna och har spelat ett par gånger. Tipsen bygger på vad jag själv har noterat i data från en algoritm av Jakub Pawlewicz som jag implementerade för "skandinavisk" yatzy för några år sedan. Jag plockade nyligen fram programmet igen efter att ha diskuterat yatzy med vännen Patrik Höglund, som experimenterar med att lära neurala nät spela. Tack Patte!
Mina rekommendationer skiljer sig från gängse strategi för amerikansk yatzy, vilket förklaras av skillnader i reglerna. Till exempel har vi två extra kategorier (Ett Par och Två Par), högre bonus, och räknar prickar på kåk i stället för att ha ett fast poängtal. Det här gör att det blir både lättare och viktigare för oss att få bonus, och att vi överlag fokuserar mer på femmor och sexor.
1. Säkra bonusen!
Ska du vinna i yatzy så ska du se till att få de 50 bonuspoängen, så är det bara. Vad du bör tänka på är att det är mycket viktigare att få många femmor och sexor än att få många ettor. Om du till exempel får 6-4-2-1-1 i första slaget, så spara sexan, inte ettorna! Detta har också att göra med att kombinera chanserna: Sparar du sexan kan du få en annan bra kombination, till exempel ett högt tvåpar eller en bra kåk.
Ett tidigt fyrtal i femmor eller sexor gör att du kan chansa friare i fortsättningen (se punkt 6). Se till att ta det ovanför strecket, inte på Fyrtal!
2. Håll koll på hur du ligger till för bonus!
Gränsen för bonus ligger vid 63 poäng, vilket är vad du får med tre av varje på fälten Ettor till Sexor. Du kan därför enkelt hålla koll på läget genom att jämföra med det. Om du till exempel får 20 på femmor, innebär det att du ligger +5. Skulle du sedan nöja dig med 1 poäng på Ettor, ligger du fortfarande +3, och så vidare. En tumregel är att aldrig hamna på minus med detta räknesätt. Det går förstås inte att garantera, men med en bra strategi ska du sällan riskera att missa bonusen.
Du behöver inte bestämma dig för att försöka få en viss sak och samla till det. Spara hellre bra tärningar och se vad det blir. Om du till exempel får 6-5-2-2-1 i allra första slaget, så spara 6-5! Då kan du nästa gång bestämma om du ska satsa på femmor, sexor eller både-och.
Det är sällan man ska spara mot en straight. Undantaget är om du får 5-4-3-2. Då lönar det sig ofta att försöka sig på en straight eftersom du har chansen till både Stor och Liten. Dock är det bra om du i så fall har någon idé om vad du ska göra de nästan hälften av gångerna då detta misslyckas (se till exempel punkt 5 och 6!).
4. Spara inte på småkrafs!
Som redan har antytts bör du oftast inte spara låga par såvida du inte behöver en viss siffra för bonusen. I skandinavisk yatzy är det bara Yatzy som ger något annat än summan av de ingående tärningarna. Stegarna har förstås en fast poäng, men det du fyller i på Ett Par, Tvåpar, Tretal, Fyrtal, Kåk och Chans bör domineras av fyror, femmor och sexor. En kombination som 6-6-1-1 hör hemma på Ett Par eller Ettor, inte på Tvåpar. Mot slutet av partiet kan du dock få nöja dig med att överhuvudtaget få poäng, i synnerhet på Kåk och Fyrtal.
5. Chans är ingen slaskhög!
Använd inte Chans bara som en utväg när du inte får någon bra kombination! Fältet Chans bör helst ge minst 21 poäng. Sitter du med bara skräp efter tredje kastet är det oftast bättre att till exempel stryka Liten Straight.
Å andra sidan ska du inte vara rädd för att "slösa bort" Chans tidigt om du får bra poäng. Får du 6-6-5-4-3 tidigt, så tag Chansen! Ett Par kommer du att få igen.
6. Ettor kan vara en bra slaskhög!
Om du ligger bra till för bonus, till exempel för att du tidigt har fått 24 poäng på Sexor, kan du med fördel använda fältet Ettor som "fallskärm" efter misslyckade försök att få svårare kombinationer. Ettor kan i sig ge max 5 poäng, så om inte bonusen är i fara är det i regel bättre att stryka Ettor än att till exempel ta futtiga 17 poäng på Chans. Det här är anledningen till att du kan chansa friare om du tidigt säkrar bonusen.
7. Stryk smart!
Att behöva stryka är förstås inte roligt, men det är bara i riktigt festliga fall du kan få hela protokollet ifyllt. För det mesta kommer du att missa några kategorier, men det gör dina motståndare också. Du kan tjäna viktiga poäng genom att stryka i tid!
Om bonusen är säkrad kan du ibland offra Ettor, men i annat fall kan du behöva stryka ett svårare fält när du hade kunnat få poäng på ett lättare. Nöj dig inte med 12 poäng på Tvåpar om du i stället kan stryka Liten Straight!
Jag har ett vagt minne av att jag en gång behövde förklara för mina kära släktingar att jag inte alls var sur och att jag visst ville fortsätta spela, efter att jag hade strukit Liten Straight i första omgången!
Men Pawlewicz' algoritm ger mig upprättelse: Blir du sittande med till exempel 6-4-3-3-1 efter första omgången och säger "Äsch, 6 poäng på treor!" så har du valt det sjätte bästa alternativet. Att stryka Liten Straight är bäst. Därefter kommer att ta 1 poäng på Ettor, att stryka Stor Straight, att ta 17 på Chans, samt att ta 6 på Ett Par.
8. Var inte rädd för att stryka Yatzy!
Det bär emot att behöva stryka Yatzy. Det är liksom att ge upp spelets idé, det hörs ju på namnet. Och tänk bara nesan att sedan få Yatzy och så har man redan strukit det!
Att stryka Yatzy är dock inte som att offra kungen i schack. Du kan vinna ändå, till och med över en motståndare som har fått Yatzy. 50 poäng känns mycket, men det är faktiskt inte så ovanligt att det äts upp av övriga poäng. Nu låter det som om jag säger tvärtemot vad jag sa nyss om bonusen, men skillnaden är att du inte kan spara ihop till en Yatzy. Du kan inte öka Yatzychanserna särskilt mycket genom att offra annat.
Chansen att få Yatzy på en omgång (tre kast) är ungefär 4.6%. Även om du bara satsade på Yatzy genom hela spelet, skulle chansen att lyckas nätt och jämnt komma över 50%.
9. Överblick: Siffror, Lätta, Svåra, och Yatzy.
Ett sätt att överblicka de femton fälten på spelplanen är att gruppera dem i Siffror, Lätta, Svåra, och Yatzy. Sifferfälten är Ettor till Sexor. Därefter har vi fyra lätta fält: Ett Par, Tvåpar, Tretal och Chans (även om Chans står längre ner i protokollet). Dessa fält kommer du nästan alltid att få poäng på. Sedan kommer fyra svåra fält: Fyrtal, Liten och Stor Straight, och Kåk. Här kommer du oftast att behöva göra någon eller ett par strykningar. Slutligen har vi det svåraste fältet av alla, Yatzy!
Om du tänker så, kan du hålla reda på vilka fält du har kvar och ungefär hur du ligger till. Ett sätt att grovt hålla koll på spelarnas chanser är att utgå från att alla får bonus och att alla får poäng på de lätta fälten. Sedan blir de svåra fälten mer utslagsgivande. I väldigt runda slängar är det 20 poäng per svårt fält. Och förstås 50 för Yatzy.
10. Ta ut målvakten? Två svåra kompenserar Yatzy!
Som vi har varit inne på kan det vara dumt att ha Yatzy kvar till sist eftersom du blir utan poäng 19 gånger av 20. Å andra sidan kanske du behöver 50 poäng för att komma ikapp den som leder. Att spara Yatzy till sist är lite som att ta ut målvakten. Det ger chansen att vända ett underläge, men oftast lyckas det inte.
Om du ligger bra till kan det vara bättre att stryka Yatzy tidigare (inte för tidigt dock, yatzyrutan är värd betydligt mer tidigare i spelet!). Men om någon annan redan har fått Yatzy, ger jag då inte i praktiken upp mina chanser att vinna? Här kan en tumregel vara att du har rimliga chanser att slå en motspelare som har fått yatzy om du klarar två svåra fält mer. Det räcker inte riktigt i sig, men oftast är det så att den som har fler strykningar också har sämre poäng på de lätta fälten.
Äsch. nu blev det precis tio punkter. Vad fånigt!
Tuesday, June 20, 2017
Misslyckad penisbluff
I maj i år publicerade tidskriften Cogent Social Sciences en märklig artikel av filosofen Peter Boghossian och matematikern James Lindsay. Artikeln har titeln The conceptual penis as a social construct, och förklarar bland annat att penisen bäst förstås som en social konstruktion snarare än anatomiskt.
Samtidigt beskrev artikelförfattarna på bloggen skeptic.com hur de avsiktligt hade skapat en nonsenstext i syfte att avslöja genusvetenskapen som ideologiskt styrd och ovetenskaplig.
Detta så kallade conceptual penis hoax gick dock rejält snett. Som redan har påpekats, till exempel här, här, och här, är Cogent Social Sciences en medioker tidskrift av den typ där författarna förväntas betala för publicering. Att man där får in en nonsensartikel tyder ingalunda på något problem hos just genusvetenskapen, utan bekräftar bara vad vi akademiker redan visste, nämligen att det slarvas med granskningen på många håll.
Den som inte känner till floran av "vetenskapliga" tramspublikationer kanske då invänder att det här väl måste ta priset, och att det nog ändå säger någonting om genusvetenskapen när man publicerar så uppenbart svammel. Men nej, det gör det inte. Träsket av skräptidskrifter med påstådd “peer review” är verkligen bottenlöst och trotsar alla ämnesgränser. Och penisbluffen är inte i närheten av något pris.
Ett annat uppmärksammat exempel är den tio sidor långa artikeln Get me off your fucking mailing list, där textmassan endast består av upprepningar av denna titel. Denna “artikel” accepterades år 2014 av tidskriften International Journal of Advanced Computer Technology efter påstådd peer review (men drogs tillbaka av den förvånade “författaren”).
Publiceringshetsen och förlagens möjligheter att mjölka forskningsinstitutioner på skattepengar driver på mot en marknad där vi bland skräppublikationerna finner hela skalan från datorgenererat blaj upp till hederlig men misslyckad forskning. Jag skulle som matematiker kunna peka ut artiklar med den matematiska jargongens motsvarighet till den konceptuella penisen, publicerade av väletablerade förlag, och som inte ens är fejkade.
Genom åren har jag i olika sammanhang diskuterat sådana gränslöst dumma men ändå efter peer review publicerade artiklar inom mitt eget och angränsande områden som fysik och datavetenskap. Men jag tror aldrig att det har föresvävat någon att dessa publikationer skulle peka mot bristande vetenskaplighet generellt inom matematik, teknik eller naturvetenskap. Många som flabbade åt Get me off your fucking mailing list noterade förmodligen inte ens att den hörde till fältet datavetenskap. Detta var uppenbart oväsentligt.
Men nu var det genusteori som Boghossian och Lindsay gjorde parodi på. Och det slog an något hos dem som retar sig på feminism och genus. Äntligen tyckte de sig kunna påvisa hur alltigenom tramsigt detta är.
Bland dem som tog chansen fanns Göteborgs-Postens ledarskribent David Eberhard. Han dundrade näven i bordet och krävde att man "rensar upp i genusdårskapen". “Ett litet axplock i det postmodernistiska flödet kan illustrera hur illa det är ställt med vetenskapligheten inom området”, påstår han.
Nej, det kan det inte. Eller för att vara mer precis, ett sådant axplock påvisar ingenting. Eberhard citerade ett antal genusartiklar, men frågan blir varför han inte passade på att i samma veva vederlägga matematik, naturvetenskap och sitt eget ämne medicin genom en snabb googling på till exempel "nonsense publication".
Ett verkligt problem är dock allmänhetens och många av mina forskarkollegors överdrivna förtroende för den granskningsprocess som kallas “peer review”. Denna process innebär att någon eller ett par forskare anonymt och utan ersättning ombeds granska en inskickad artikel, och deras rapporter förblir konfidentiella. Trots att processen undandrar sig insyn, och trots de otaliga exemplen där det har gått snett, betraktas peer review som en gold standard för vetenskaplig kvalitet.
Historien om den konceptuella penisartikeln är intressant på flera plan. Man kan fråga sig vad det beror på att genusforskningen pekas ut som ovetenskaplig på basis av en bluffartikel och att historien valsar runt på sociala medier där var och varannan kommentator anser sig kunna bedöma hela detta fält, samtidigt som matematik, teknik och naturvetenskap verkar stå över motsvarande misstankar.
Nu har den aktuella bluffartikeln som sagt redan kritiserats från många håll, men det är inte första gången genusvetenskapen ifrågasätts med citat som påstås "tala för sig själva". För cirka tio år sedan trendade genus som ett buzzword inom forskningsansökningar, något som till exempel bloggaren Tanja Bergkvist (egentligen med rätta) retade sig på. I Svenska Dagbladet raljerade hon över forskningsprojektet Trumpeten som genussymbol, med utdrag ur projektansökningen. Artiklar om detta forskningsprojekt har delats flera gånger på facebook av trumpetande vänner, och jag gissar att det är ett av de mest hånade projekten i Vetenskapsrådets historia.
Jag kan inte uttala mig om kvaliteten på trumpetprojektet, men så vitt jag kan se handlar det om forskning i musikhistoria som åtminstone faktiskt har bedrivits. Frågan är varför det inte blir rabalder på debattsidorna vartenda år när forskare i till exempel mitt och Bergkvists ämne matematik får anslag för modeord som bioinformatik (trendade runt millennieskiftet) eller big data (på senare år), när det i vissa fall kan misstänkas att de sökande inte ens känner till att begreppen i fråga finns på riktigt. Vad beror det på att vissa forskare hudflängs i media, medan andra kommer undan?
Kan vi verkligen utesluta den ironiska möjligheten att genusfaktorer spelar in i detta?
Det är oklart vad kritikerna anser är fel med genusvetenskapen och vad den av Eberhard efterfrågade "upprensningen'' skulle bestå i. Ovannämnda utbud av skräpartiklar är en konsekvens av en internationell fri marknad, där den enda upprensning vi kan göra är att påverka svenska myndigheter att sluta betala för eländet (hur och varför vi fortsätter att betala är en annan diskussion).
Ska genusteorin rensas ut för att genusfrågor är oviktiga? Fast tanken att skillnaderna mellan män och kvinnor är så små att de av den anledningen inte förtjänar att studeras är inte vad till exempel Eberhard annars brukar föra fram.
Eller är problemet helt enkelt att de som forskar i genusteori är för dåliga på det? Då blir frågan varför inte bättre forskare tar över spelplanen och konkurrerar ut de sämre. Borde vi kanske satsa mer pengar på genusvetenskap för att därigenom locka starkare forskare? Borde Eberhards rubrik i stället ha varit "Rusta upp i genusvetenskapen"?
En ytterligare möjlighet är att genusforskningen har hamnat i ett låst läge där mediokra forskare styr och sätter normerna, medan starkare forskare på grund av dessa normer inte kan hävda sig. Menar Eberhard att det därför krävs en "upprensning" där man bryter mönstret genom att politiskt tillsätta tjänster avsedda för dessa starkare forskare, trots att de enligt gängse inomvetenskapliga kriterier är sämre meriterade?
Detta är en intressant tanke, och man kan fråga sig om sådana låsningar kan ha uppstått tidigare, inom andra akademiska discipliner.
Samtidigt beskrev artikelförfattarna på bloggen skeptic.com hur de avsiktligt hade skapat en nonsenstext i syfte att avslöja genusvetenskapen som ideologiskt styrd och ovetenskaplig.
Detta så kallade conceptual penis hoax gick dock rejält snett. Som redan har påpekats, till exempel här, här, och här, är Cogent Social Sciences en medioker tidskrift av den typ där författarna förväntas betala för publicering. Att man där får in en nonsensartikel tyder ingalunda på något problem hos just genusvetenskapen, utan bekräftar bara vad vi akademiker redan visste, nämligen att det slarvas med granskningen på många håll.
Den som inte känner till floran av "vetenskapliga" tramspublikationer kanske då invänder att det här väl måste ta priset, och att det nog ändå säger någonting om genusvetenskapen när man publicerar så uppenbart svammel. Men nej, det gör det inte. Träsket av skräptidskrifter med påstådd “peer review” är verkligen bottenlöst och trotsar alla ämnesgränser. Och penisbluffen är inte i närheten av något pris.
Ett annat uppmärksammat exempel är den tio sidor långa artikeln Get me off your fucking mailing list, där textmassan endast består av upprepningar av denna titel. Denna “artikel” accepterades år 2014 av tidskriften International Journal of Advanced Computer Technology efter påstådd peer review (men drogs tillbaka av den förvånade “författaren”).
Publiceringshetsen och förlagens möjligheter att mjölka forskningsinstitutioner på skattepengar driver på mot en marknad där vi bland skräppublikationerna finner hela skalan från datorgenererat blaj upp till hederlig men misslyckad forskning. Jag skulle som matematiker kunna peka ut artiklar med den matematiska jargongens motsvarighet till den konceptuella penisen, publicerade av väletablerade förlag, och som inte ens är fejkade.
Genom åren har jag i olika sammanhang diskuterat sådana gränslöst dumma men ändå efter peer review publicerade artiklar inom mitt eget och angränsande områden som fysik och datavetenskap. Men jag tror aldrig att det har föresvävat någon att dessa publikationer skulle peka mot bristande vetenskaplighet generellt inom matematik, teknik eller naturvetenskap. Många som flabbade åt Get me off your fucking mailing list noterade förmodligen inte ens att den hörde till fältet datavetenskap. Detta var uppenbart oväsentligt.
Men nu var det genusteori som Boghossian och Lindsay gjorde parodi på. Och det slog an något hos dem som retar sig på feminism och genus. Äntligen tyckte de sig kunna påvisa hur alltigenom tramsigt detta är.
Bland dem som tog chansen fanns Göteborgs-Postens ledarskribent David Eberhard. Han dundrade näven i bordet och krävde att man "rensar upp i genusdårskapen". “Ett litet axplock i det postmodernistiska flödet kan illustrera hur illa det är ställt med vetenskapligheten inom området”, påstår han.
Nej, det kan det inte. Eller för att vara mer precis, ett sådant axplock påvisar ingenting. Eberhard citerade ett antal genusartiklar, men frågan blir varför han inte passade på att i samma veva vederlägga matematik, naturvetenskap och sitt eget ämne medicin genom en snabb googling på till exempel "nonsense publication".
Ett verkligt problem är dock allmänhetens och många av mina forskarkollegors överdrivna förtroende för den granskningsprocess som kallas “peer review”. Denna process innebär att någon eller ett par forskare anonymt och utan ersättning ombeds granska en inskickad artikel, och deras rapporter förblir konfidentiella. Trots att processen undandrar sig insyn, och trots de otaliga exemplen där det har gått snett, betraktas peer review som en gold standard för vetenskaplig kvalitet.
Historien om den konceptuella penisartikeln är intressant på flera plan. Man kan fråga sig vad det beror på att genusforskningen pekas ut som ovetenskaplig på basis av en bluffartikel och att historien valsar runt på sociala medier där var och varannan kommentator anser sig kunna bedöma hela detta fält, samtidigt som matematik, teknik och naturvetenskap verkar stå över motsvarande misstankar.
Nu har den aktuella bluffartikeln som sagt redan kritiserats från många håll, men det är inte första gången genusvetenskapen ifrågasätts med citat som påstås "tala för sig själva". För cirka tio år sedan trendade genus som ett buzzword inom forskningsansökningar, något som till exempel bloggaren Tanja Bergkvist (egentligen med rätta) retade sig på. I Svenska Dagbladet raljerade hon över forskningsprojektet Trumpeten som genussymbol, med utdrag ur projektansökningen. Artiklar om detta forskningsprojekt har delats flera gånger på facebook av trumpetande vänner, och jag gissar att det är ett av de mest hånade projekten i Vetenskapsrådets historia.
Jag kan inte uttala mig om kvaliteten på trumpetprojektet, men så vitt jag kan se handlar det om forskning i musikhistoria som åtminstone faktiskt har bedrivits. Frågan är varför det inte blir rabalder på debattsidorna vartenda år när forskare i till exempel mitt och Bergkvists ämne matematik får anslag för modeord som bioinformatik (trendade runt millennieskiftet) eller big data (på senare år), när det i vissa fall kan misstänkas att de sökande inte ens känner till att begreppen i fråga finns på riktigt. Vad beror det på att vissa forskare hudflängs i media, medan andra kommer undan?
Kan vi verkligen utesluta den ironiska möjligheten att genusfaktorer spelar in i detta?
Det är oklart vad kritikerna anser är fel med genusvetenskapen och vad den av Eberhard efterfrågade "upprensningen'' skulle bestå i. Ovannämnda utbud av skräpartiklar är en konsekvens av en internationell fri marknad, där den enda upprensning vi kan göra är att påverka svenska myndigheter att sluta betala för eländet (hur och varför vi fortsätter att betala är en annan diskussion).
Ska genusteorin rensas ut för att genusfrågor är oviktiga? Fast tanken att skillnaderna mellan män och kvinnor är så små att de av den anledningen inte förtjänar att studeras är inte vad till exempel Eberhard annars brukar föra fram.
Eller är problemet helt enkelt att de som forskar i genusteori är för dåliga på det? Då blir frågan varför inte bättre forskare tar över spelplanen och konkurrerar ut de sämre. Borde vi kanske satsa mer pengar på genusvetenskap för att därigenom locka starkare forskare? Borde Eberhards rubrik i stället ha varit "Rusta upp i genusvetenskapen"?
En ytterligare möjlighet är att genusforskningen har hamnat i ett låst läge där mediokra forskare styr och sätter normerna, medan starkare forskare på grund av dessa normer inte kan hävda sig. Menar Eberhard att det därför krävs en "upprensning" där man bryter mönstret genom att politiskt tillsätta tjänster avsedda för dessa starkare forskare, trots att de enligt gängse inomvetenskapliga kriterier är sämre meriterade?
Detta är en intressant tanke, och man kan fråga sig om sådana låsningar kan ha uppstått tidigare, inom andra akademiska discipliner.
Saturday, June 17, 2017
13532385396179, the number which is its own prime factorization
Here is how you could, until just a couple of weeks ago, have made a thousand dollars by solving a math problem. The problem, with a bounty from John Conway, has to do with the prime factorization of integers. Take a number like \[120245675.\] This number, broken down to its prime factors, becomes
\[5 \cdot 5\cdot 11\cdot 17 \cdot 17 \cdot 17 \cdot 89.\]
Here we have sorted the factors from smaller to larger, and using exponent notation we can write the factorization as \[5^2\cdot 11 \cdot 17^3 \cdot 89.\]
Conway's weird idea was to consider the factorization itself as a new number by just reading the digits, including the exponents, from left to right:
\[521117389.\]
This would probably be frowned upon by many of my mathematician colleagues ("so typical of Conway!" I hear them say), who would point out that the operation is completely artificial and depends on writing the numbers in base 10.
But Conway is famous for inventing scientifically silly-looking puzzles and then asking (and answering!) extremely deep questions about them. He is the inventor of the famous Game Of Life that is believed to have wasted a substantial fraction of the world's computational resources in the last three decades of the twentieth century. Less well known is that, using Life-patterns discovered by various enthusiasts, he proved that basic questions about the game are undecidable in the sense of Turing and Gödel, and that self-replicating structures can be built in the game. And when he studied some simple two-person games, he happened to discover an amazingly rich theory of infinite numbers, now called the surreal numbers.
Anyway, Conway considered the function $f$ that maps a number to its prime-factorization-sorted-with-exponents-dropped-interpreted-in-base-10. And by the way, no, I don't think that this one will challenge the foundations of mathematics or the philosophy of science.
His 1000-dollar question was about what happens if we start with a number, apply the function $f$, and repeat.
If $N$ is a prime, then $f(N)=N$ and that's that. But for most other numbers, $f(N) > N$. For instance, the number $283439$ is certainly larger than $283\cdot 439$, since the former is more than 1000 times $283$ while the latter is only $439$ times $283$. And therefore $f(283\cdot 439) > 283\cdot 439$. It's easy to find examples where $f(N)<N$, like $f(512)=29$, but they require $N$ to have relatively few prime factors where at least one occurs to a power.
If we start from a number like 18, then in 3 steps we will reach 232, 2329, and 17137, which is prime. But if we start from 20, then after 50 iterations we will have reached a 66-digit (still non-prime) number with the numbers increasing in every step, and it seems entirely possible that the numbers will grow without limit, never reaching a prime.
There are deep and very precise results in number theory explaining how often one should expect to hit primes in a randomly increasing sequence of numbers. Basically the "probability" of a number being prime is inversely proportional to the number of digits, which means that a sequence that "only" grows exponentially can be expected to contain infinitely many primes, while slightly faster growing sequences might very well not contain any.
Iterating Conway's function will (under some assumptions of the numbers behaving like "average" numbers) lead to one of those sequences that grow just a smidgeon faster than exponentially (as long as it doesn't encounter a prime), so when it comes to iterating from a number like 20, it's not even clear (to me) what to guess based on the statistical properties of prime factorization.
This is what might have motivated Conway to award 1000 dollars for the proof or disproof of the statement that iterating $f$ starting from any integer $\geq 2$ will eventually lead to a prime. Just to demonstrate that silly looking problems can be extremely hard.
Nevertheless, the problem was recently solved by James Davis, an amateur mathematician, and there is already a Numberphile video on this.
What Davis decided to try was to refute Conway's conjecture by constructing a non-prime number $N$ for which $f(N)=N$.
On the whole, almost all numbers have their largest prime factor occurring to power 1 in their prime factorization. So it seems reasonable to search for an $N$ that ends in the digits of its largest prime factor, and Davis restricted his search to such numbers.
At first, this seems a bit weird. Could, for instance, a number that ends in the digits $7993$ be divisible by $7993$? Well, certainly! If we multiply $7993$ by anything divisible by $10000$, like $640000$, we will get a number that ends in four zeros. If we then add $7993$, making it $640001\cdot 7993$, we get a number, in this case $5115527993$, that ends in $7993$ and has $7993$ as one of its prime factors. This particular number doesn't give a counterexample to the Conway conjecture, but at least we have a method for finding candidates.
Now we could try all four digit primes say, and multiply them with numbers ending in 0001, checking whether we get a counterexample. But we can do even better. If instead we start from a number like $640001$, we can ask what it would take for a four digit prime $p$ to provide a counterexample of the form \[f(640001\cdot p) = 640001\cdot p.\]
Perhaps we can figure out what $p$ will have to be, instead of searching through all four-digit primes.
What we can do is to look at the prime factorization of the number $640001$. Provided all factors of $640001$ are smaller than $p$, $f(640001\cdot p)$ will consist of the digits of $f(640001)$ followed by the digits of $p$, which is \[f(640001)\cdot 10000 + p.\]
The equation \[f(640001)\cdot 10000 + p = 640001\cdot p\] now simplifies to
\[\frac{f(640001)}{64} = p.\]
The number $640001$ factorizes as $29^2\cdot 761$, which means that $f(640001) = 292761$. Since \[\frac{292761}{64}\] isn't even an integer, let alone a prime, we don't have to look further but can move on to computing \[\frac{f(650001)}{65}\] and so on.
This is what Davis did. Presumably he started by looking for a two-digit final prime, discovering the near-miss \[ \frac{f(1701)}{17} = \frac{f(3^5\cdot 7)}{17} = \frac{357}{17} = 21,\] that provides the equation \[35721 = 3^5\cdot 7 \cdot 21.\] If only $21$ had been a prime...
Then he moved on to searching for 3-, 4-, and 5-digit final primes, and eventually got to
\[\frac{f(140700001)}{1407} = \frac{f(13\cdot 53^2 \cdot 3853)}{1407} =\frac{135323853}{1407} = 96179.\]
Perhaps this was a moment of Bingo! rather than Heureka, but anyway, 96179 is not only a five-digit integer as required, but also a prime. Therefore the number
\[13532385396179 = 13\cdot 53^2\cdot 3853 \cdot 96179\] refutes the Conway conjecture.
The geeky part of me just loves weird coincidences like this one. I mean forget about $111111111^2$ and the multiplication table of $142857$, those are just what we expect in view of algebra, but this...
I don't know exactly in what order Davis was searching, but finding the counterexample must have taken no more than a tiny fraction of a second of computer time, since only a few thousand cases would need to be tried.
This perhaps doesn't seem too hard in retrospect, but to find it you have to dare search for the simplest type of counterexample even though it seems unlikely to exist. Notice that in order for this to work, the number $140700001$ had to have a fairly large repeated prime factor so that $f(140700001)$ becomes smaller than $140700001$, otherwise the quotient would have been greater than $10^5$ and therefore not five-digit. Then the number $f(140700001) = 135323853$, which has no simple arithmetical relation to $140700001$, had to be divisible by $1407$, and only one number in $1407$ is. Finally the quotient $96179$ had to be a prime number.
As Davis eloquently commented on MathOverflow: "The point I took away was that there exist problems that look so hard, nobody has tried anything easy".
\[5 \cdot 5\cdot 11\cdot 17 \cdot 17 \cdot 17 \cdot 89.\]
Here we have sorted the factors from smaller to larger, and using exponent notation we can write the factorization as \[5^2\cdot 11 \cdot 17^3 \cdot 89.\]
Conway's weird idea was to consider the factorization itself as a new number by just reading the digits, including the exponents, from left to right:
\[521117389.\]
This would probably be frowned upon by many of my mathematician colleagues ("so typical of Conway!" I hear them say), who would point out that the operation is completely artificial and depends on writing the numbers in base 10.
But Conway is famous for inventing scientifically silly-looking puzzles and then asking (and answering!) extremely deep questions about them. He is the inventor of the famous Game Of Life that is believed to have wasted a substantial fraction of the world's computational resources in the last three decades of the twentieth century. Less well known is that, using Life-patterns discovered by various enthusiasts, he proved that basic questions about the game are undecidable in the sense of Turing and Gödel, and that self-replicating structures can be built in the game. And when he studied some simple two-person games, he happened to discover an amazingly rich theory of infinite numbers, now called the surreal numbers.
Anyway, Conway considered the function $f$ that maps a number to its prime-factorization-sorted-with-exponents-dropped-interpreted-in-base-10. And by the way, no, I don't think that this one will challenge the foundations of mathematics or the philosophy of science.
His 1000-dollar question was about what happens if we start with a number, apply the function $f$, and repeat.
If $N$ is a prime, then $f(N)=N$ and that's that. But for most other numbers, $f(N) > N$. For instance, the number $283439$ is certainly larger than $283\cdot 439$, since the former is more than 1000 times $283$ while the latter is only $439$ times $283$. And therefore $f(283\cdot 439) > 283\cdot 439$. It's easy to find examples where $f(N)<N$, like $f(512)=29$, but they require $N$ to have relatively few prime factors where at least one occurs to a power.
If we start from a number like 18, then in 3 steps we will reach 232, 2329, and 17137, which is prime. But if we start from 20, then after 50 iterations we will have reached a 66-digit (still non-prime) number with the numbers increasing in every step, and it seems entirely possible that the numbers will grow without limit, never reaching a prime.
There are deep and very precise results in number theory explaining how often one should expect to hit primes in a randomly increasing sequence of numbers. Basically the "probability" of a number being prime is inversely proportional to the number of digits, which means that a sequence that "only" grows exponentially can be expected to contain infinitely many primes, while slightly faster growing sequences might very well not contain any.
Iterating Conway's function will (under some assumptions of the numbers behaving like "average" numbers) lead to one of those sequences that grow just a smidgeon faster than exponentially (as long as it doesn't encounter a prime), so when it comes to iterating from a number like 20, it's not even clear (to me) what to guess based on the statistical properties of prime factorization.
This is what might have motivated Conway to award 1000 dollars for the proof or disproof of the statement that iterating $f$ starting from any integer $\geq 2$ will eventually lead to a prime. Just to demonstrate that silly looking problems can be extremely hard.
Nevertheless, the problem was recently solved by James Davis, an amateur mathematician, and there is already a Numberphile video on this.
What Davis decided to try was to refute Conway's conjecture by constructing a non-prime number $N$ for which $f(N)=N$.
On the whole, almost all numbers have their largest prime factor occurring to power 1 in their prime factorization. So it seems reasonable to search for an $N$ that ends in the digits of its largest prime factor, and Davis restricted his search to such numbers.
At first, this seems a bit weird. Could, for instance, a number that ends in the digits $7993$ be divisible by $7993$? Well, certainly! If we multiply $7993$ by anything divisible by $10000$, like $640000$, we will get a number that ends in four zeros. If we then add $7993$, making it $640001\cdot 7993$, we get a number, in this case $5115527993$, that ends in $7993$ and has $7993$ as one of its prime factors. This particular number doesn't give a counterexample to the Conway conjecture, but at least we have a method for finding candidates.
Now we could try all four digit primes say, and multiply them with numbers ending in 0001, checking whether we get a counterexample. But we can do even better. If instead we start from a number like $640001$, we can ask what it would take for a four digit prime $p$ to provide a counterexample of the form \[f(640001\cdot p) = 640001\cdot p.\]
Perhaps we can figure out what $p$ will have to be, instead of searching through all four-digit primes.
What we can do is to look at the prime factorization of the number $640001$. Provided all factors of $640001$ are smaller than $p$, $f(640001\cdot p)$ will consist of the digits of $f(640001)$ followed by the digits of $p$, which is \[f(640001)\cdot 10000 + p.\]
The equation \[f(640001)\cdot 10000 + p = 640001\cdot p\] now simplifies to
\[\frac{f(640001)}{64} = p.\]
The number $640001$ factorizes as $29^2\cdot 761$, which means that $f(640001) = 292761$. Since \[\frac{292761}{64}\] isn't even an integer, let alone a prime, we don't have to look further but can move on to computing \[\frac{f(650001)}{65}\] and so on.
This is what Davis did. Presumably he started by looking for a two-digit final prime, discovering the near-miss \[ \frac{f(1701)}{17} = \frac{f(3^5\cdot 7)}{17} = \frac{357}{17} = 21,\] that provides the equation \[35721 = 3^5\cdot 7 \cdot 21.\] If only $21$ had been a prime...
Then he moved on to searching for 3-, 4-, and 5-digit final primes, and eventually got to
\[\frac{f(140700001)}{1407} = \frac{f(13\cdot 53^2 \cdot 3853)}{1407} =\frac{135323853}{1407} = 96179.\]
Perhaps this was a moment of Bingo! rather than Heureka, but anyway, 96179 is not only a five-digit integer as required, but also a prime. Therefore the number
\[13532385396179 = 13\cdot 53^2\cdot 3853 \cdot 96179\] refutes the Conway conjecture.
The geeky part of me just loves weird coincidences like this one. I mean forget about $111111111^2$ and the multiplication table of $142857$, those are just what we expect in view of algebra, but this...
I don't know exactly in what order Davis was searching, but finding the counterexample must have taken no more than a tiny fraction of a second of computer time, since only a few thousand cases would need to be tried.
This perhaps doesn't seem too hard in retrospect, but to find it you have to dare search for the simplest type of counterexample even though it seems unlikely to exist. Notice that in order for this to work, the number $140700001$ had to have a fairly large repeated prime factor so that $f(140700001)$ becomes smaller than $140700001$, otherwise the quotient would have been greater than $10^5$ and therefore not five-digit. Then the number $f(140700001) = 135323853$, which has no simple arithmetical relation to $140700001$, had to be divisible by $1407$, and only one number in $1407$ is. Finally the quotient $96179$ had to be a prime number.
As Davis eloquently commented on MathOverflow: "The point I took away was that there exist problems that look so hard, nobody has tried anything easy".
Saturday, May 6, 2017
Sverigedemokrater vs prov i samhällskunskap
Jag vill inte dela eländet på facebook, men genom Nyheter Idag kan vi få en glimt av hur samhället kommer att se ut den dag SD får makten. Tydligen har det gjorts ett nationellt prov i samhällskunskap i dagarna, där eleverna bland annat skulle ta ställning till påståenden om invandring. Påståendena var till exempel “Många flyr för att det är krig i hemlandet” och “Den främsta orsaken till migration är att människor vill sprida sin religion”.
Ett par av påståendena verkar ha fått SD-politiker att gå i taket. Påståendena, i synnerhet “De flesta flyr för att leva på bidrag och slippa arbeta” och “En vanlig orsak till migration är att man vill bygga upp terrorceller i världen” ska enligt Josef Fransson (SD) utgöra “propaganda” och “indoktrinering”. Enligt artikeln anser Jeff Ahl (SD) att det borde vara straffbart att formulera en provuppgift så.
I kommentarstråden på Nyheter Idag (facebook, offentligt) kan man se upp-och-nervända världen, där den ena kommentatorn efter den andra beklagar hur vi nu är på väg mot ett totalitärt samhälle, och hur endast SD står upp för demokrati och yttrandefrihet. Jag undrar om ens George Orwell hade kunnat fantisera fram den diskussionen.
Någon anser det “vidrigt” att bedöma detta efter vad som “anses vara fakta idag”. Det talas om hjärntvättning, åsiktsregistrering och svartmålning av SD. “Skolan är politisk”, “Skolan har gjort kunskap till något subjektivt”, “Ska alla tycka som läraren och bortse från fakta?”, “Politiskt vinklat”, “Ska de tvinga ungdomar att vara invandringspositiva?”, “Någon måste ställas till svars”, “Sjukt”, dundrar den ena efter den andra.
Här har jag för läsbarhetens skull tagit mig friheten att korrigera stavfel innanför citationstecknen, vilket jag hoppas är försvarbart då jag inte nämner någon vid namn. Ytterst få av dessa sverigevänner behärskar nämligen det svenska språket tillräckligt väl för att kunna skriva en hel mening utan stavfel.
Någon tycks mena att eftersom det går att ha en åsikt i frågan, är provet inte baserat på fakta, men här får jag lägga in en brasklapp eftersom jag egentligen inte förstår resonemanget. "Vad är rätt svar?” frågar någon retoriskt. “Vem bestämmer vad som är rätt svar?” fortsätter en annan. Flera slår fast att rätt svar är att de flesta faktiskt flyr för att leva på bidrag och slippa arbeta. Märkligt nog uppstår ingen debatt och utväxlas inga okvädesord mellan dem och å andra sidan den falang som menar att det hela är en åsiktsfråga där inget svar är rätt eller fel.
Någon utlovar inspelad uppvaktning av skolinspektionen, och jag tycker mig skönja en hotfull underton. Någon ska polisanmäla. När en kommentator hoppar in i vargflocken med “SD är ett rasistiskt parti” bryts genast den kvasiintellektuella samtalstonen och det enkla svaret “Pucko” får flera tummar upp.
Någon berättar om barndomen i en kommunistisk diktatur och hur västeuropa nu är på väg dit. Vederbörande frågar sedan retoriskt om det nu är dags “för oss som sökte skydd här att dra vidare”, till synes utan att notera någon ironi eller något paradoxalt i att som flykting vara rädd att behöva fly igen, undan de människor som INTE tror att flyktingar kommer för att leva på bidrag och slippa arbeta. Nu känns som om det blev snurrigt på grund av för många negationer i den föregående meningen, men det var nog själva idén som var snurrig.
Fast utifrån ett strikt höger-vänsterperspektiv blir det hela fullt logiskt. Den som en gång har flytt från en vänsterdiktatur är förstås på sin vakt mot extremvänsteråsikter som till exempel den att människor kan ha haft skäl att fly från diktaturer.
Jag ger mig inte in i denna kommentarstråd för att försöka undervisa, vare sig i historia, samhällskunskap eller vetenskapsteori. Men jag vill att vi andra ska vara medvetna om vad vi har att göra med här.
Det här är inte bara några omåkta gnällpellar som sitter och knyter nävarna i byxfickorna. Jeff Ahl och Josef Fransson sitter i riksdagen, och när de säger att något borde vara straffbart, så betyder det att det kommer att bli straffbart om SD får bestämma.
Risken att Jimmie Åkesson blir vald till statsminister nästa sensommar är kanske inte överhängande (peppar peppar), men ett scenario där SD blir enskilt största parti känns nu inte alls orealistiskt.
Vi kommer då att leva i ett samhälle där den starkaste politiska rörelsen verkar för att akademiker och ämnesexperter ska riskera att fällas i domstol och straffas om de redovisar fakta eller skapar skolmaterial som inte ligger i linje med partiets ideologi.
Jag är matematiker, och matematiken kanske inte ligger i den främsta skottlinjen, men jag drivs ändå av en förtjusning i att söka och att påtala fakta, särskilt om de går emot min egen och andra människors magkänsla. Bland de 349 som ska styra vårt samhälle sitter det nu folk och säger att sådana som jag ska straffas. Den SD-svans som fortfarande framstår som lite patetisk med sina hot om att tillkalla polis och skolinspektion, har reella möjligheter att genom sina folkvalda få inflytande över dessa och andra myndigheter.
Det paradoxala och kanske mest skrämmande är att denna rörelse tycks drivas av vreden och kraften hos den som anser sig slå uppåt. Den har beslutsamheten, övertygelsen, och när den får makten förmodligen även hämndbegäret, hos människor som anser sig kuvade och som anser sig behöva slå sig fria från ett förtryckande storebrorssamhälle. “Nu jävlar får det vara nog med akademikernas och journalisternas trakasserande av våra styrande politiker med denna fördömda forskning och dessa förbannade fakta. Straffas ska de, för vi har faktiskt demokrati och yttrandefrihet i det här landet, det är inget 1984-samhälle det här”.
Nja, det där var egentligen inget citat, utan min egen sarkasm. Men, direkt från ovannämnda diskussionstråd och utan stavnings- och grammatikkorrigering:
"någon som ser likheter mellan nordkorea och vart sverige är påväg."
Japp.
krig är fred
frihet är slaveri
okunskap är styrka
Saturday, April 1, 2017
Myndighetspolicy om helvetets existens?
"Nej, inte fan heller", säger ansvarig minister Anna Ekström på frågan om helvetet finns.
Det vore någonting det, att skriva om en dag som idag.
Men tyvärr fortsätter daltandet med religiösa trosföreställningar, vilket gör det svårare att försvara myndigheters hållning gentemot trossamfund och kan få dessa myndigheter att framstå som lika fundamentalistiska som de samfund de har att göra med.
Nu har vi nya turer i diskussionen om statligt stöd till religiösa organisationer som till exempel sprider misogyni och homofobi.
Föreningen Sveriges Förenade Muslimer har enligt en granskning av Sofie Löwenmark på Smedjan genom åren fått miljontals kronor i stöd från myndigheten för ungdoms- och civilsamhällesfrågor (MUCF). Föreningen har flera gånger bjudit in föreläsaren Muadh Zamzam som hävdar att 12-13-åriga flickor måste "täcka sig" för att inte hamna i helvetet. På kritiska frågor om varför ett barn ska få höra detta, svarar han i en video från 2014 att "det är så här det funkar. Ska vi ljuga för henne?" och "Det är gud som bestämmer vem som hamnar i helvetet, jag har inte nyckeln". Uppringd av Aftonbladet säger han senare att "man måste kolla på hela föreläsningen", vilket verkar vara den här videon.
Flera debattörer, utöver Sofie Löwenmark även Erik Helmerson, Jonas Gardell, och tidigare Magnus Ranstorp anser att denna förening bör bli av med sitt statliga stöd, vilket jag förstås håller med om.
Men finns helvetet? Är det någon som vet? Och kan en myndighet som MUCF ta ställning?
Debattörer är upprörda och politiker ska granska och se över, men ingenstans ser jag någon av dem hävda att Zamzam har fel. Det är liksom underförstått självklart, men ingen törs säga det rakt ut. Möjligen påpekar någon att hans påståenden saknar stöd i koranen, vilket i sammanhanget är irrelevant eftersom MUCF ändå inte baserar sina beslut på denna skrift.
Representanter för det sekulära samhället tenderar att bli försiktiga när gud och helvetet kommer på tal. Vi är nog många som genom en synbarligen icke-religiös uppfostran har fått lära oss att ingen vet om gud finns eller vad som händer med själen efter döden, samt att vetenskapen i princip inte kan ge oss svar på dessa frågor.
Enligt detta sätt att tänka kan naturvetenskapen visserligen påvisa att universum är mellan 13 och 14 miljarder år gammalt, att människokroppen är uppbyggd av de slags atomer som finns i marken, vattnet och luften, och att vi är släkt med växterna och djuren. Men den anses inte kunna hjälpa oss i frågor om gud, om varför universum finns, om moraliskt rätt och fel, eller om människans själ och vad som händer med den efter döden.
En vanlig uppfattning, om än ofta outtalad, är nog att myndighetsutövning ska ske med denna grundsyn för att vara neutral i trosfrågor. Ett eventuellt beslut att dra in stödet till Sveriges Förenade Muslimer skulle därför bygga enbart på att deras verksamhet inte är i linje med principer om till exempel jämställdhet, medan myndigheten undviker att ta ställning i fråga om deras tro. Och MUCF har också ett uttalat krav på att föreningar som får stöd "följer demokratins idéer" och att verksamheten "är förenlig med principen om alla människors lika värde".
Problemet är att vi målar in oss i ett väldigt konstigt hörn om vi kritiserar religiösa föreningar för att de skrämmer barn med helvetet, samtidigt som vi lämnar walk-over i frågan huruvida helvetet verkligen finns och huruvida världen faktiskt är beskaffad på sådant sätt att flickor hamnar där om de inte fogar sig i en patriarkal struktur.
Det blir absurt att säga att det visserligen mycket väl skulle kunna finnas en gud som straffar ledigt klädda kvinnor med evig förbannelse, men att vi med hänvisning till feministisk ideologi ändå ska dra in det statliga stödet till den som lär ut detta. Om Zamzams lära vore sann, skulle vi då verkligen vara beredda att i jämställdhetens namn utsätta miljoner själar för guds gränslösa vrede och tortyr? Notera hur feminismen framstår som oresonlig om man först är villig att kompromissa om helvetet.
Vad det egentligen handlar om är förstås kvinnors situation till exempel i områden som Tensta. Men om vi först inte ens vågar avfärda fundamentalistiska idéer om helvetet, blir det svårt att sedan komma någonstans med rationella argument.
Så vitt jag kan se måste kritiken mot Muadh Zamzam och Sveriges Förenade Muslimer därför i princip bottna även i att vi avfärdar deras lära om helvetet som osann, inte bara i att den strider mot vår uppfattning om jämställdhet. Annars trasslar vi snart in oss i våra egna argument. För att inte tala om den dubbeltydiga signal vi sänder till muslimska ungdomar.
Men skulle detta gå ihop med religionsfriheten? Och är inte idén att helvetet inte finns också bara en tro bland andra? Inte kan vi väl låta myndighetsbeslut baseras på sådant?
Jodå, det går alldeles utmärkt, och är i själva verket är den enda hållning som går att försvara. Religionsfrihet innebär för det första inte att man inte får säga att någon har fel. Det innebär bara att vi inte trakasserar människor för att de tror på något, ens om det de tror på inte stämmer.
För det andra kan en vetenskaplig grundsyn vägleda oss även utanför laboratorier och lektionssalar. En princip som har blivit känd som Hitchens rakkniv säger till exempel att vad som görs gällande utan evidens kan avfärdas utan evidens. Man behöver inte kunna hänvisa till direkta undersökningar av helvetets eventuella egenskaper för att avfärda Muadh Zamzams påståenden. Att rapporter om sådana undersökningar saknas beror helt enkelt på att det aldrig har funnits något att undersöka.
Jag ska inte fördjupa mig i vetenskapsteori, utan bara påpeka att myndigheter redan idag baserar beslut på sådan avsaknad av evidens. Om jag ansöker hos läkemedelsverket om att få en ny påstådd mirakelkur mot cancer godkänd och inga försöksresultat finns som vare sig stöder eller motsäger mina påståenden, så blir metoden inte godkänd. Läkemedelsverkets policy, som baseras på vetenskaplighet, vore givetvis omöjlig att försvara om varje fråga i brist på evidens ansågs lika öppen åt båda håll. Men det är inte så att man med hänvisning till en fundamentalistisk doktrin avfärdar en metod som kanske fungerar, utan den vetenskapliga hållningen innebär att vi i avsaknad av evidens bedömer det som uteslutet att metoden skulle fungera.
Det är inte alltid enkelt att avgöra vad som kan accepteras utan vidare efterforskning, men ett liknande förhållningssätt vore fullt rimligt även gentemot religiösa föreställningar, och vore helt förenligt med ett sekulärt samhälle, religionsfrihet, och en myndighetsutövning baserad på en vetenskaplig grundsyn.
Jag menar inte att MUCF ska motivera enskilda beslut med resonemang om helvetet, men tassandet på tå inför religiösa vanföreställningar i den (nu igen) aktuella debatten är både onödigt och kontraproduktivt.
En sak till förresten, helvetet finns inte!
Tuesday, March 14, 2017
Pi-day, with quotes from Wigner and Knuth
Eugene Wigner's famous essay The Unreasonable Effectiveness of Mathematics in the Natural Sciences from 1960 (which has its own wikipedia page) begins with a story about the unexpected appearance of the number $\pi$ in statistics:
THERE IS A story about two friends, who were classmates in high school, talking about their jobs. One of them became a statistician and was working on population trends. He showed a reprint to his former classmate. The reprint started, as usual, with the Gaussian distribution and the statistician explained to his former classmate the meaning of the symbols for the actual population, for the average population, and so on. His classmate was a bit incredulous and was not quite sure whether the statistician was pulling his leg. "How can you know that?" was his query. "And what is this symbol here?" "Oh," said the statistician, "this is pi." "What is that?" "The ratio of the circumference of the circle to its diameter." "Well, now you are pushing your joke too far," said the classmate, "surely the population has nothing to do with the circumference of the circle."
All students of statistics encounter this appearance of $\pi$ in the density function \[\frac1{\sqrt{2\pi}}\cdot e^{-x^2/2}\] of the normal distribution. The number $\pi$ enters because the probability of getting exactly $n$ heads and $n$ tails when flipping a coin $2n$ times is \[\frac12\cdot \frac34 \cdot \frac56 \cdot \cdots \cdot \frac{2n-1}{2n},\] which (for large $n$) is approximately \[ \frac1{\sqrt{\pi n}}.\]
In his talk "Why Pi?" from December 2010, Donald Knuth said about this (10-11 minutes into the video) that
This has always been a mystery, I think to everybody, why pi should occur... . It seemed to be one of those strange coincidences or facts of nature that there's a constant, and lo and behold, it agrees with pi... . However, two years ago a guy in Sweden named Johan Wästlund figured out why.
Happy pi-day to everyone!
Sunday, February 19, 2017
Morfar
Idag är det 100 år sedan min morfar Gunnar Westman föddes. Han var varm och omtänksam, och som Einar Nauclér uttryckte det i en minnesruna, en till anden rikt begåvad hedersman.
Vi barnbarn minns väl framförallt sommardagarna i stugan nedanför Multråberget i Sollefteå med honom och mormor Margit. Morfar slog gräsplätten vid stugan med lie, och i början av 80-talet var det både Wimbledontennis och fotbolls-VM där. Såvida det inte var längdhopp i slänten ner mot Bodéns handelsträdgård, eller orienteringstävling. Morfar var gammal orienterare och gjorde en lagom svår bana åt oss.
För morfar var botanik ett stort intresse, och luppen och floran låg ofta framme på köksbordet i stugan. Jag tänker ibland att det är från morfar jag har fått mitt intresse för vetenskap. Det handlade inte bara om att skilja ett grässtrå från ett annat, utan det bottnade i ett brett intresse och en stor respekt för naturen.
Morfar jobbade på datacentralen i Sundsvall, och jag var där på besök en gång när jag var ganska liten. Jag fick se datamaskinerna och fick med mig några hålkort som souvenir. Morfar hade arbetat där sedan 1961 och lär väl ha varit bland de första norrlänningarna att handskas med datorer.
Någon gång strax efter vår flytt till Falun 1977 hittade jag en bok om matematik på stadsbiblioteket. Det fanns ett avsnitt om magiska kvadrater med exempel av storlek 3 gånger 3 och 5 gånger 5. Jag undrade om det gick att göra en magisk kvadrat av storlek 4 gånger 4, och frågade pappa om man kunde få summan 34 överallt. Pappa var lite fundersam och undrade hur jag visste att det skulle bli just 34. På något sätt hade jag listat ut det, men kunde inte förklara hur. Vi kom i alla fall fram till att vi nog måste ringa till morfar när vi hade ett så knepigt matematiskt problem. Morfar bad att få fundera en stund och återkomma. Och mycket riktigt hade han hittat en lösning. Men han ville inte avslöja den på en gång. Lite skulle jag få tänka ut själv. Efter att han hade berättat vilka tal som skulle stå i några rutor, insåg jag att om jag bara fick veta ett tal till, skulle resten gå att räkna ut. Jag lyckades förhandla till mig ett tal till, och kunde därefter fylla i hela kvadraten.
Fylla i kvadrater i form av korsord gjorde han för övrigt gärna. Då hände det ofta att uppslagsböckerna kom fram. Uppslagsverket var uppenbarligen väl använt, för det fanns marginalanteckningar och instuckna tidningsurklipp på var och varannan sida. I bokhyllan fanns även några böcker om matematik och naturvetenskap, bland andra Ett två tre... oändligheten av George Gamow, som gjorde djupt intryck på mig.
För morfar var det viktigt att läsa, utbilda sig, och hålla sig informerad. Han hade inte haft möjlighet att studera vidare i sin ungdom, men tog gymnasieexamen på 1970-talet och fick en alldeles egen åktur på lastbilsflak till barnbarnens förtjusning.
Morfar berättade ibland om evakueringen av Karelen senvintern 1940. Han deltog som lastbilsförare i en svensk lastbilskonvoj som hjälpte till. Något organiserat boende fanns inte, utan man fick improvisera. En natt sov morfar tillsammans med några finnar på en båt. De hade inget gemensamt språk, men det fanns ett schackspel, och enligt morfar spelade de schack halva natten.
Någon gång i 7-8 årsåldern hade jag börjat intressera mig för detta spel, och morfar hade ju spelat en del, om än inte på tävlingsnivå. I vårt första parti rockerade jag kort som svart. Morfar gick till angrepp och satte matt med damen på h7 understödd av löpare. Jag såg matthotet komma och tänkte att jag borde ha flyttat undan tornet från f8 för att ge plats åt kungen, men jag hade ställt det andra tornet på e8 så det gick inte. Den här minnesbilden finns kvar, men så här i efterhand är det lite oklart för mig varför inte något bondedrag hade kunnat stoppa det omedelbara hotet. I vårt följande möte fick jag i alla fall revansch, och under de kommande somrarna blev statistiken så småningom 4-1 till mig.
Morfar berättade gärna, både om växter och natur, och om gamla original. Och vi lyssnade andäktigt på historierna om Pip-Otto, 'n Sven Wikström från Brattbäcken, 'n Lång Nyber' och de andra. Det var oftast på mål. Eftersom vi hade hört dem förut började vi skratta innan poängen kom, och morfar skrattade också så tårarna rann: "Mära, ho' äter bara när ho' står still", "Hä' bar' te å följ dyng-ranna", "No' vet du vem Korea är, det är ju käringa åt 'n Port-Artur", "Nu du Jensch-Daniel, nu lure' ja' dig styggt!", "Å när de kom till andra sidan, hade de miljoners miljoner på varje finger", "Soophie, ta å sätt på kaffepanna, 'n Sven Wikström från Brattbäcken är här", "Å då gick ja te'n tôck'n dän geolog. Å unnersökte huvve mitt", "Lugn gott folk, det här ä 'n Sven Wikström från Brattbäcken, å han flyt' på plåmboka!".
Morfar ledde ibland botaniska exkursioner för den intresserade allmänheten. Han och mormor var en gång ute och förberedde en sådan utflykt. Morfar, som då var över 80 år, la märke till någon intressant växt som dock bara kunde nås genom att man klättrade ner för en ganska besvärlig brant. Han begav sig i alla fall ner, medan mormor stod kvar. Mormor, som kunde bli lite otålig när hon behövde vänta, ropade då ner till honom "Men Gunnar, du kan int' ta dem ner dit, de är ju gamla!"
Vi barnbarn minns väl framförallt sommardagarna i stugan nedanför Multråberget i Sollefteå med honom och mormor Margit. Morfar slog gräsplätten vid stugan med lie, och i början av 80-talet var det både Wimbledontennis och fotbolls-VM där. Såvida det inte var längdhopp i slänten ner mot Bodéns handelsträdgård, eller orienteringstävling. Morfar var gammal orienterare och gjorde en lagom svår bana åt oss.
För morfar var botanik ett stort intresse, och luppen och floran låg ofta framme på köksbordet i stugan. Jag tänker ibland att det är från morfar jag har fått mitt intresse för vetenskap. Det handlade inte bara om att skilja ett grässtrå från ett annat, utan det bottnade i ett brett intresse och en stor respekt för naturen.
Morfar jobbade på datacentralen i Sundsvall, och jag var där på besök en gång när jag var ganska liten. Jag fick se datamaskinerna och fick med mig några hålkort som souvenir. Morfar hade arbetat där sedan 1961 och lär väl ha varit bland de första norrlänningarna att handskas med datorer.
Någon gång strax efter vår flytt till Falun 1977 hittade jag en bok om matematik på stadsbiblioteket. Det fanns ett avsnitt om magiska kvadrater med exempel av storlek 3 gånger 3 och 5 gånger 5. Jag undrade om det gick att göra en magisk kvadrat av storlek 4 gånger 4, och frågade pappa om man kunde få summan 34 överallt. Pappa var lite fundersam och undrade hur jag visste att det skulle bli just 34. På något sätt hade jag listat ut det, men kunde inte förklara hur. Vi kom i alla fall fram till att vi nog måste ringa till morfar när vi hade ett så knepigt matematiskt problem. Morfar bad att få fundera en stund och återkomma. Och mycket riktigt hade han hittat en lösning. Men han ville inte avslöja den på en gång. Lite skulle jag få tänka ut själv. Efter att han hade berättat vilka tal som skulle stå i några rutor, insåg jag att om jag bara fick veta ett tal till, skulle resten gå att räkna ut. Jag lyckades förhandla till mig ett tal till, och kunde därefter fylla i hela kvadraten.
Fylla i kvadrater i form av korsord gjorde han för övrigt gärna. Då hände det ofta att uppslagsböckerna kom fram. Uppslagsverket var uppenbarligen väl använt, för det fanns marginalanteckningar och instuckna tidningsurklipp på var och varannan sida. I bokhyllan fanns även några böcker om matematik och naturvetenskap, bland andra Ett två tre... oändligheten av George Gamow, som gjorde djupt intryck på mig.
För morfar var det viktigt att läsa, utbilda sig, och hålla sig informerad. Han hade inte haft möjlighet att studera vidare i sin ungdom, men tog gymnasieexamen på 1970-talet och fick en alldeles egen åktur på lastbilsflak till barnbarnens förtjusning.
Morfar berättade ibland om evakueringen av Karelen senvintern 1940. Han deltog som lastbilsförare i en svensk lastbilskonvoj som hjälpte till. Något organiserat boende fanns inte, utan man fick improvisera. En natt sov morfar tillsammans med några finnar på en båt. De hade inget gemensamt språk, men det fanns ett schackspel, och enligt morfar spelade de schack halva natten.
Någon gång i 7-8 årsåldern hade jag börjat intressera mig för detta spel, och morfar hade ju spelat en del, om än inte på tävlingsnivå. I vårt första parti rockerade jag kort som svart. Morfar gick till angrepp och satte matt med damen på h7 understödd av löpare. Jag såg matthotet komma och tänkte att jag borde ha flyttat undan tornet från f8 för att ge plats åt kungen, men jag hade ställt det andra tornet på e8 så det gick inte. Den här minnesbilden finns kvar, men så här i efterhand är det lite oklart för mig varför inte något bondedrag hade kunnat stoppa det omedelbara hotet. I vårt följande möte fick jag i alla fall revansch, och under de kommande somrarna blev statistiken så småningom 4-1 till mig.
Morfar berättade gärna, både om växter och natur, och om gamla original. Och vi lyssnade andäktigt på historierna om Pip-Otto, 'n Sven Wikström från Brattbäcken, 'n Lång Nyber' och de andra. Det var oftast på mål. Eftersom vi hade hört dem förut började vi skratta innan poängen kom, och morfar skrattade också så tårarna rann: "Mära, ho' äter bara när ho' står still", "Hä' bar' te å följ dyng-ranna", "No' vet du vem Korea är, det är ju käringa åt 'n Port-Artur", "Nu du Jensch-Daniel, nu lure' ja' dig styggt!", "Å när de kom till andra sidan, hade de miljoners miljoner på varje finger", "Soophie, ta å sätt på kaffepanna, 'n Sven Wikström från Brattbäcken är här", "Å då gick ja te'n tôck'n dän geolog. Å unnersökte huvve mitt", "Lugn gott folk, det här ä 'n Sven Wikström från Brattbäcken, å han flyt' på plåmboka!".
Morfar ledde ibland botaniska exkursioner för den intresserade allmänheten. Han och mormor var en gång ute och förberedde en sådan utflykt. Morfar, som då var över 80 år, la märke till någon intressant växt som dock bara kunde nås genom att man klättrade ner för en ganska besvärlig brant. Han begav sig i alla fall ner, medan mormor stod kvar. Mormor, som kunde bli lite otålig när hon behövde vänta, ropade då ner till honom "Men Gunnar, du kan int' ta dem ner dit, de är ju gamla!"
Monday, February 13, 2017
Pythagoras schackproblem
Pythagoras sats säger som bekant att sidorna i en rätvinklig triangel uppfyller ekvationen
\[a^2 + b^2 = c^2.\] Det innebär till exempel att en triangel med sidorna 3 och 4 i rät vinkel har hypotenusa kvadratroten ur 9+16, vilket är exakt 5.
På schackbrädet betyder det att om vi mäter avstånd från mittpunkten på rutorna, så ligger exempelvis rutan e5 på avstånd exakt 5 rutor från b1, eftersom den ligger tre steg år höger (i alla fall sett från vits håll) och fyra steg rakt fram.
Jag har under alla år betraktat detta som enbart en konsekvens av Pythagoras sats, och trott att det enklaste sättet att inse att avståndet är 5 är att ta ett rutat papper och rita en kvadrat vars sidor går tre steg i en riktning och fyra steg i den andra, och räkna ut att arean är 25 rutor. Det är ju så man bevisar Pythagoras sats.
Även om jag väl inte har grubblat över det dagligen, så har det stört mig något att man tycks behöva använda area för att definiera avstånd. Avstånd borde ju vara ett mer fundamentalt begrepp. Men det finns ingen symmetri hos brädet som direkt visar att det är lika långt från b1 till e5 som från b1 till b6 eller g1.
Den typ av symmetri jag menar är till exempel den som visar att alla springardrag är lika långa. Den vita springare som startar på b1 har till exempel ett lika långt hopp till a3 som till c3. Det ser vi eftersom man kan spegla rutsystemet i b-linjen. Det är även lika långt till d2 som till c3, vilket följer av att man kan spegla i diagonalen b1-h7. För att riktigt säkerställa dessa likheter i längd bortom allt tvivel noterar vi också att rutsystemet kan roteras 90 grader runt b1 så att rutan a3 överförs till d2.
Häromdagen insåg jag plötsligt att det finns ett sätt att direkt se att sträckan b1-e5 är lika med sträckan b1-g1. Alltså så att det blir uppenbart även för ögat. Nu kanske jag är fånig och har missat något som egentligen var självklart, men jag hade inte tänkt på det här förut. Och då har jag ändå multiplicerat några komplexa tal i mina dagar och förstås noterat att $(2+i)^2 = 3+4i$ medan $(2+i)(2-i) = 5$. Men även komplex multiplikation är väl att betrakta som mer sofistikerat än avstånd.
Så låt mig presentera Pythagoras schackproblem. Vit drar och gör matt i tre drag:
Den pythagoreiska springaren gör här tre hopp och landar lika långt från sitt utgångsläge i de båda huvudvarianterna. Dess väg är utstakad med de svarta pjäserna för att illustrera symmetrin mellan att gå från b1 till e5 respektive från b1 till g1 (men samtliga pjäser fyller också en funktion i problemet!). Det finns även några så kallade icke-tematiska varianter, men vits drag är unika hela vägen.
\[a^2 + b^2 = c^2.\] Det innebär till exempel att en triangel med sidorna 3 och 4 i rät vinkel har hypotenusa kvadratroten ur 9+16, vilket är exakt 5.
På schackbrädet betyder det att om vi mäter avstånd från mittpunkten på rutorna, så ligger exempelvis rutan e5 på avstånd exakt 5 rutor från b1, eftersom den ligger tre steg år höger (i alla fall sett från vits håll) och fyra steg rakt fram.
Jag har under alla år betraktat detta som enbart en konsekvens av Pythagoras sats, och trott att det enklaste sättet att inse att avståndet är 5 är att ta ett rutat papper och rita en kvadrat vars sidor går tre steg i en riktning och fyra steg i den andra, och räkna ut att arean är 25 rutor. Det är ju så man bevisar Pythagoras sats.
Även om jag väl inte har grubblat över det dagligen, så har det stört mig något att man tycks behöva använda area för att definiera avstånd. Avstånd borde ju vara ett mer fundamentalt begrepp. Men det finns ingen symmetri hos brädet som direkt visar att det är lika långt från b1 till e5 som från b1 till b6 eller g1.
Den typ av symmetri jag menar är till exempel den som visar att alla springardrag är lika långa. Den vita springare som startar på b1 har till exempel ett lika långt hopp till a3 som till c3. Det ser vi eftersom man kan spegla rutsystemet i b-linjen. Det är även lika långt till d2 som till c3, vilket följer av att man kan spegla i diagonalen b1-h7. För att riktigt säkerställa dessa likheter i längd bortom allt tvivel noterar vi också att rutsystemet kan roteras 90 grader runt b1 så att rutan a3 överförs till d2.
Häromdagen insåg jag plötsligt att det finns ett sätt att direkt se att sträckan b1-e5 är lika med sträckan b1-g1. Alltså så att det blir uppenbart även för ögat. Nu kanske jag är fånig och har missat något som egentligen var självklart, men jag hade inte tänkt på det här förut. Och då har jag ändå multiplicerat några komplexa tal i mina dagar och förstås noterat att $(2+i)^2 = 3+4i$ medan $(2+i)(2-i) = 5$. Men även komplex multiplikation är väl att betrakta som mer sofistikerat än avstånd.
Så låt mig presentera Pythagoras schackproblem. Vit drar och gör matt i tre drag:
Den pythagoreiska springaren gör här tre hopp och landar lika långt från sitt utgångsläge i de båda huvudvarianterna. Dess väg är utstakad med de svarta pjäserna för att illustrera symmetrin mellan att gå från b1 till e5 respektive från b1 till g1 (men samtliga pjäser fyller också en funktion i problemet!). Det finns även några så kallade icke-tematiska varianter, men vits drag är unika hela vägen.
Lösningen börjar 1. Sxd2+, och därefter 2. Sxf3+ vad än svart gör. Detta andra drag är schack oavsett var svart har ställt kungen i första draget: står den på e1 är det schack från vits springare, och står den på e2, f2 eller g2, är det avdragsschack från tornet. Svart måste flytta kungen igen, och efter drag 2 finns det fem rutor svart kan ha gått till: På Kd1, Kf1 eller Kh1 sätter vit matt med Td2, Dc1 respektive Th2. Detta är dock bara "bivarianter". De två tematiska varianterna är 2. - Kg3 3. Sxe5 och 2. - Kh3 3. Sxg1.
Ett springarhopp kan ju betraktas som två steg i en riktning följt av ett steg i 90 graders vinkel mot de första. Pythagoras springare gör på tre drag ett springarhopp av springarhopp. Och även alla sådana måste vara lika långa. I springarens värld finns alltså den symmetri jag tyckte mig sakna!
Nu kanske problemkonnässörerna invänder mot att vit schackar i vartenda drag och slår pjäser till höger och vänster. Men problemschack är ju en konstform. Då kan man även välja att bryta så hårt det går mot reglerna, och slå den svarta damen med schack i inledningsdraget. Jag kunde ha ställt någon annan pjäs på d2, men nu blev det exakt en pjäs av varje sort förutom bönder. Kanske finns det ändå en viss elegans i alla schackarna samt i att problemet tack vare avsaknaden av bönder fungerar under alla schackbrädets ovannämnda symmetrier!
Ett springarhopp kan ju betraktas som två steg i en riktning följt av ett steg i 90 graders vinkel mot de första. Pythagoras springare gör på tre drag ett springarhopp av springarhopp. Och även alla sådana måste vara lika långa. I springarens värld finns alltså den symmetri jag tyckte mig sakna!
Nu kanske problemkonnässörerna invänder mot att vit schackar i vartenda drag och slår pjäser till höger och vänster. Men problemschack är ju en konstform. Då kan man även välja att bryta så hårt det går mot reglerna, och slå den svarta damen med schack i inledningsdraget. Jag kunde ha ställt någon annan pjäs på d2, men nu blev det exakt en pjäs av varje sort förutom bönder. Kanske finns det ändå en viss elegans i alla schackarna samt i att problemet tack vare avsaknaden av bönder fungerar under alla schackbrädets ovannämnda symmetrier!
Friday, February 10, 2017
Bulletin Of Genuine Unbiased Science (special issue on theological number theory)
There is widespread support, both among laypeople and researchers, for the system called “peer-review” as a way of certifying the quality of published scientific papers. This must be one of the dumbest ideas that the scientific community has ever produced.
Having your peers discuss your work is great, but that's not what “peer-review” is about. For readers not familiar with the process, it means that when a paper is submitted to a journal, the journal editors will send it to one or two other researchers (the peers) asking them for their opinion about the paper. The reports and the identities of the reviewers remain confidential, and the editors still decide whether or not to publish the paper.
There was nothing wrong with this idea in the first place. The problem is the ridiculous weight assigned to the process. The concept has reached the general public, and more than once I have been lectured on it by non-academics who seem to think that peer-review (or the lack of it) is how we know that homeopathy doesn't work. And within academia, if you apply for a job, a promotion or a research grant, publications that aren't "peer-reviewed" are systematically dismissed.
"Peer-review" is now regarded as an integral part of the scientific method, alongside with diametrically opposite ideas such as openness and skepticism towards unverifiable claims.
The fact that the reviewers remain anonymous is often cited as a reason to trust them, because it means they didn't have to be afraid to criticize the paper. An interesting comparison (that can't be taken too far of course) is the use of anonymous testimony in courts, which has been discussed recently in Sweden. Here the traditional view is the opposite, that a testimony can't be trusted if it's anonymous.
But here is the paradox: If you are suspicious of the quality of a paper to the point that you doubt it’s good even when you are told that it has an author, then how can you possibly become convinced when you get the additional information that it was “peer-reviewed”? This to me makes no sense.
It’s like maintaining a policy of never buying a car unless the salesperson says they asked a person on the street what they thought about it. You don't care who that person were or what they actually said, and you have no means of verifying it anyway, but you maintain a picture of that person as unbiased and therefore trustworthy, and you absolutely insist that the salesperson must say that they asked somebody.
To me it makes more sense just to decide that a Volvo is probably ok.
It’s true that an author might be biased towards thinking that their own paper is great. But at least they put their name on it and gambled a chunk of their reputation. The reviewer is an anonymous person with no incentive to do a good job.
I could go on about how the process is slow and inefficient, and how “peer-review” is used as an excuse for throwing away tax payers’ money on ridiculously expensive journals. By the way, Michael Nielsen has written some interesting stuff about both pros and cons of the system. But the point I’d like to make here is that it’s dangerous to promote “peer-review” as a remedy against fake news and bogus science. I see memes like “What to we want? Evidence-based science! When do we want it? After peer-review!” posted on the internet, and I see claims that only a hundred or so peer-reviewed papers (out of many thousands) cast doubt on anthropogenic global warming.
This makes me think of Goodhart's law: When a measure becomes a target, it ceases to be a good measure. Peer-review is already unreliable, but if we keep promoting it as a gold standard of science, it will also become corrupt, because it's too easy to fake.
We must realize that the fact that the reviewers are anonymous and their reports confidential means we have no way of verifying that those reports even existed, let alone that they endorsed the results. Again I could go on about papers being published without a report or despite reviewers being extremely negative.
But just imagine, out of the many weird things that might happen, that Donald Trump would start his own journal of climate science, claiming it was peer-reviewed. If you insisted for years that climate change denial doesn't hold under peer-review, then what would you do?
The problem is that if you were to question the claim that “We’ve got the greatest people folks, reviewers and really they’re fabulous, and they have the best reviews, believe me.”, then you would be applying double standards. Not good if you claim to be defending the scientific method. You never asked for the reports or the names of the reviewers from any other journal.
And you don’t even need any money in order to start a journal. Heck, I could start my own journal on this blog, claiming it’s peer-reviewed. Again if you make fun of me, suggesting that my peer-review process doesn’t adhere to scientific standards, then the joke is on you, because you just fell victim to confirmation bias.
So let me introduce the Bulletin Of Genuine Unbiased Science (BOGUS), and the special issue on theological number theory.
Paper 0. Proof of the existence of a Largest Prime Number
Abstract: We establish the existence of the Largest Prime Number.
Theorem 0: The Largest Prime Number exists.
Proof: This is derived as a Corollary of the following Lemma.
Lemma 1: Everything exists.
Proof: No counterexample can exist.
Having your peers discuss your work is great, but that's not what “peer-review” is about. For readers not familiar with the process, it means that when a paper is submitted to a journal, the journal editors will send it to one or two other researchers (the peers) asking them for their opinion about the paper. The reports and the identities of the reviewers remain confidential, and the editors still decide whether or not to publish the paper.
There was nothing wrong with this idea in the first place. The problem is the ridiculous weight assigned to the process. The concept has reached the general public, and more than once I have been lectured on it by non-academics who seem to think that peer-review (or the lack of it) is how we know that homeopathy doesn't work. And within academia, if you apply for a job, a promotion or a research grant, publications that aren't "peer-reviewed" are systematically dismissed.
"Peer-review" is now regarded as an integral part of the scientific method, alongside with diametrically opposite ideas such as openness and skepticism towards unverifiable claims.
The fact that the reviewers remain anonymous is often cited as a reason to trust them, because it means they didn't have to be afraid to criticize the paper. An interesting comparison (that can't be taken too far of course) is the use of anonymous testimony in courts, which has been discussed recently in Sweden. Here the traditional view is the opposite, that a testimony can't be trusted if it's anonymous.
But here is the paradox: If you are suspicious of the quality of a paper to the point that you doubt it’s good even when you are told that it has an author, then how can you possibly become convinced when you get the additional information that it was “peer-reviewed”? This to me makes no sense.
It’s like maintaining a policy of never buying a car unless the salesperson says they asked a person on the street what they thought about it. You don't care who that person were or what they actually said, and you have no means of verifying it anyway, but you maintain a picture of that person as unbiased and therefore trustworthy, and you absolutely insist that the salesperson must say that they asked somebody.
To me it makes more sense just to decide that a Volvo is probably ok.
It’s true that an author might be biased towards thinking that their own paper is great. But at least they put their name on it and gambled a chunk of their reputation. The reviewer is an anonymous person with no incentive to do a good job.
I could go on about how the process is slow and inefficient, and how “peer-review” is used as an excuse for throwing away tax payers’ money on ridiculously expensive journals. By the way, Michael Nielsen has written some interesting stuff about both pros and cons of the system. But the point I’d like to make here is that it’s dangerous to promote “peer-review” as a remedy against fake news and bogus science. I see memes like “What to we want? Evidence-based science! When do we want it? After peer-review!” posted on the internet, and I see claims that only a hundred or so peer-reviewed papers (out of many thousands) cast doubt on anthropogenic global warming.
This makes me think of Goodhart's law: When a measure becomes a target, it ceases to be a good measure. Peer-review is already unreliable, but if we keep promoting it as a gold standard of science, it will also become corrupt, because it's too easy to fake.
We must realize that the fact that the reviewers are anonymous and their reports confidential means we have no way of verifying that those reports even existed, let alone that they endorsed the results. Again I could go on about papers being published without a report or despite reviewers being extremely negative.
But just imagine, out of the many weird things that might happen, that Donald Trump would start his own journal of climate science, claiming it was peer-reviewed. If you insisted for years that climate change denial doesn't hold under peer-review, then what would you do?
The problem is that if you were to question the claim that “We’ve got the greatest people folks, reviewers and really they’re fabulous, and they have the best reviews, believe me.”, then you would be applying double standards. Not good if you claim to be defending the scientific method. You never asked for the reports or the names of the reviewers from any other journal.
And you don’t even need any money in order to start a journal. Heck, I could start my own journal on this blog, claiming it’s peer-reviewed. Again if you make fun of me, suggesting that my peer-review process doesn’t adhere to scientific standards, then the joke is on you, because you just fell victim to confirmation bias.
So let me introduce the Bulletin Of Genuine Unbiased Science (BOGUS), and the special issue on theological number theory.
Paper 0. Proof of the existence of a Largest Prime Number
Abstract: We establish the existence of the Largest Prime Number.
Theorem 0: The Largest Prime Number exists.
Proof: This is derived as a Corollary of the following Lemma.
Lemma 1: Everything exists.
Proof: No counterexample can exist.
Thursday, January 12, 2017
På något sätt måste detta få ett stopp!?
Nu tycker tydligen en majoritet av det svenska folket att tiggeri åter bör förbjudas. Men om jag förstår henne rätt, anser Lena Mellin på Aftonbladet att det mest anmärkningsvärda i sammanhanget är att var sjätte svensk “tycker att det är okej att människor sitter i snömodden och tigger”. Jag är inte ens i närheten av att få någon rätsida på den formuleringen. Ja, det är mycket jag tycker är "okej" i den meningen att det inte bör vara olagligt eller straffbart. Till exempel att halka och dratta på ändan i snömodden. Men snömodden lär ju bli var tiggeriet hamnar om det förbjuds.
Det verkar vara en fråga för regeringen. “På något sätt måste detta få ett stopp”, sa Stefan Löfven i en intervju i december.
Så låt oss fundera lite på exakt vad det är vi retar oss på och varför, och vad det är vi vill förbjuda. Ska röda korset, frälsningsarmén, cancerfonden och musikhjälpen förbjudas? Nja, det handlar nog snarare om själva beteendet utanför affärer och på andra platser där många människor rör sig.
Som järnvägsstationer till exempel.
Häromdagen satt jag på ett fik på centralstationen i Göteborg och väntade på ett tåg. Jag fick då tillfälle att under några minuter iaktta en grupp av 4-5 män i 25-årsåldern som stod precis utanför. De var uppenbart vuxna och yrkesarbetande, men betedde sig som ett gäng tonårspojkar som var ute på stan utan mamma för första gången.
Högljudda och skräniga gick de omkring och gjorde olika poser och vrålflabbade åt varandras skämt. De hade ställt sig i en passage där folk måste förbi för att komma till tågen, och de betedde sig som om de ägde detta utrymme.
De unga männen ställde sig i vägen för människor som uppenbart bara ville förbi, till synes oförmögna att läsa av folks irriterade ansiktsuttryck. En medelålders man blev närgånget adresserad “Tjeeena killen!”. Kvinnor fick “Tjejen, hallååå tjejen!” efter sig på ett sätt som gränsar till så kallad catcalling.
Vilka är det så som beter sig på detta sätt? Är det fotbollshuliganer, eller slödder från utanförskapsområden?
Nej, det är marknadsföring från Tre och Mobilizera.
Vad man vill åstadkomma, utöver att skämma ut sina varumärken, begriper jag inte, och jag kan bara spekulera i vad de vill signalera:
Jag tänker lite irriterat att en järnvägsstation är en viktig punkt i infrastrukturen, där en bör kunna ta sig fram utan att bli ofredad.
Och mycket riktigt. En romsk kvinna går långsamt förbi. Ingen av grabbarna ställer sig i vägen för henne. Inget "Hallååå tjejen!".
Och någon logik finns det väl. Hon borde ju inte få vara där, tycker en majoritet av det svenska folket. Ska hon åtalas för lösdriveri, eller bara köras ut i snömodden? Regeringen grubblar vidare.
Det verkar vara en fråga för regeringen. “På något sätt måste detta få ett stopp”, sa Stefan Löfven i en intervju i december.
Så låt oss fundera lite på exakt vad det är vi retar oss på och varför, och vad det är vi vill förbjuda. Ska röda korset, frälsningsarmén, cancerfonden och musikhjälpen förbjudas? Nja, det handlar nog snarare om själva beteendet utanför affärer och på andra platser där många människor rör sig.
Som järnvägsstationer till exempel.
Häromdagen satt jag på ett fik på centralstationen i Göteborg och väntade på ett tåg. Jag fick då tillfälle att under några minuter iaktta en grupp av 4-5 män i 25-årsåldern som stod precis utanför. De var uppenbart vuxna och yrkesarbetande, men betedde sig som ett gäng tonårspojkar som var ute på stan utan mamma för första gången.
Högljudda och skräniga gick de omkring och gjorde olika poser och vrålflabbade åt varandras skämt. De hade ställt sig i en passage där folk måste förbi för att komma till tågen, och de betedde sig som om de ägde detta utrymme.
De unga männen ställde sig i vägen för människor som uppenbart bara ville förbi, till synes oförmögna att läsa av folks irriterade ansiktsuttryck. En medelålders man blev närgånget adresserad “Tjeeena killen!”. Kvinnor fick “Tjejen, hallååå tjejen!” efter sig på ett sätt som gränsar till så kallad catcalling.
Vilka är det så som beter sig på detta sätt? Är det fotbollshuliganer, eller slödder från utanförskapsområden?
Nej, det är marknadsföring från Tre och Mobilizera.
Vad man vill åstadkomma, utöver att skämma ut sina varumärken, begriper jag inte, och jag kan bara spekulera i vad de vill signalera:
Behöver du teknisk support? Vår personal mansplainar gärna, och kollar garanterat aldrig upp något, för vi anställer bara ungtuppar som tror att de redan kan allt.eller
Saknar du atmosfären i killarnas omklädningsrum på högstadiet? Sök jobb hos oss!eller möjligen
Vill du ha dressing i ansiktet och en papperspåse på huvudet? Fråga oss om mobiltelefoni!
Jag tänker lite irriterat att en järnvägsstation är en viktig punkt i infrastrukturen, där en bör kunna ta sig fram utan att bli ofredad.
Och mycket riktigt. En romsk kvinna går långsamt förbi. Ingen av grabbarna ställer sig i vägen för henne. Inget "Hallååå tjejen!".
Och någon logik finns det väl. Hon borde ju inte få vara där, tycker en majoritet av det svenska folket. Ska hon åtalas för lösdriveri, eller bara köras ut i snömodden? Regeringen grubblar vidare.
Subscribe to:
Comments (Atom)