Men det började med att Bo "bosjo" Sjögren frågade Olle hur man kan bedöma vem som är bäst på att tippa stryktips av två personer som, i stället för att bara välja 1, X eller 2 på varje match, får sätta procentsatser på de tre utfallen. Diskussionen kom att involvera logaritmer, entropi, begreppet ärlighet, Avogadros tal, och McCutcheonvarianten (en spelöppning i schack som verkar omges av en sorts kult). Den lär även ha renderat mig en nominering till Svenska Besserwisserföreningens hangaroundavdelning, men det är oklart om jag blev invald.
Nåväl, idén är att om till exempel person A ger utfallen 1, X och 2 sannolikheterna 55%, 20%, 25%, medan B säger 40%, 25%, 35%, och det sedan slutar med att hemmalaget vinner (alltså en etta), tyder detta på att A var lite bättre än B, i och med att A angav högre sannolikhet (55%) än B gjorde (40%) för det som faktiskt hände. Hade i stället bortalaget vunnit, skulle vi ha haft viss anledning att tro att B var bättre på att tippa.
Men om vi skulle låta A och B ange procenttal i 13 matcher och helt sonika addera de tal som tilldelats matchernas faktiska utfall, skulle det löna sig, för den som vill framstå som duktig på att tippa, att sätta 100% på det utfall man betraktar som mest sannolikt. Vi kunde då lika gärna ha låtit A och B tippa varsin rad på vanligt sätt.
Olles svar var att i stället addera logaritmerna av procenttalen. Ett värdigt besserwissersvar (notera att epitetet besserwisser har positiv klang i Olles värld), men hur motiverar man detta utan att gräva ner sig i analys och sannolikhetsteori?
En kommentator vid namn Norpan föreslog vad som ser ut att vara ekvivalent, nämligen att multiplicera procenttalen och låta produkten bli respektive tippares poängtal. Att addera logaritmer är ju enligt räknelagarna detsamma som att först multiplicera talen och sedan logaritmera, så man borde kunna jämföra tipparskickligheten hos A och B genom att jämföra produkterna av deras procenttal.
Med Norpans förslag räcker det med mellanstadiematematik, men kruxet är att om man försöker maximera väntevärdet av sin poäng, lönar det sig fortfarande att sätta 100% på det man tror mest på, trots att detta oftast ger noll poäng i slutändan! Problemet gick till slut att lösa utan logaritmer, men det jag tänkte prata om här är ett kortspel som modellerar situationen. Jag kallar det för Besserwisserpoker, och den som vill veta varför får titta på Olles blogg.
Spelet går ut på att gissa vilken av tre pokerhänder som blir starkast. De två spelarna A och B startar med ett rejält antal marker, minst tio tusen var. Kanske hundra tusen är bättre, för de kommer att försvinna snabbt! Man får ha något slags växlingssystem.
I varje runda blandar man en vanlig kortlek och delar ut tre händer med två kort vardera som i pokervarianten Texas Holdem, samt en "flopp" bestående av tre gemensamma kort. Baserat på dessa kort (som båda spelarna ser) fördelar varje spelare sina marker mellan de tre händerna. Dessa satsningar görs "simultant" i den meningen att varje spelare måste bestämma sin fördelning av marker utan att se hur motståndaren gör.
Därefter (och spelarna får nu se hur motståndaren satsade) delar man ut ytterligare två gemensamma kort. I poker kallas dessa traditionellt turn och river. Styrkan hos var och en av de tre händerna bestäms nu, precis som i Texas Holdem, av den bästa pokerhand som går att åstadkomma genom att välja ut fem av de sju tillgängliga korten (de två på respektive hand samt de fem gemensamma).
När det har konstaterats vilken eller vilka av de tre händerna som är starkast, får spelarna tillbaka de marker som satsades på dessa händer. Vinnaren är den som efter 13 omgångar har flest marker kvar, eller som i ett tidigare skede har marker kvar när motståndarens marker har tagit slut.
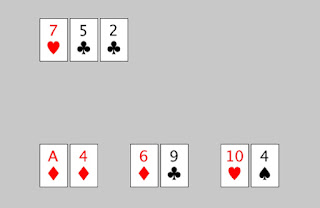
När man har delat ut en giv, kan det till exempel se ut så här:
Ingen hand har något par, så hand 1 är för tillfället starkast i kraft av sitt ess. Det kan i förstone verka som om händerna 2 och 3 är ungefär lika starka. Men hand 2 har förutom möjligheten till ett par också stegdrag, och litet färgdrag, alltså möjlighet till stege om det kommer en åtta, eller färg om det kommer två klövrar. Hand 3 å andra sidan är dominerad av hand 1 i den meningen att om det kommer en fyra, är hand 1 fortfarande bättre, och får hand 3 stege, så får hand 1 också stege.
Kontentan blir att hand 2 är nästan lika bra som hand 1, medan hand 3 ligger betydligt sämre till. Det finns $43\cdot 42 / 2 = 903$ möjligheter för de sista två gemensamma korten, och ett litet datorprogram räknar ut att hand 1 vinner ensam 444 gånger (mindre än hälften!), hand 2 vinner ensam 353 gånger, och hand 3 vinner ensam bara 84 gånger. 22 gånger får man pengarna tillbaka på både hand 1 och hand 3.
Hur ska man då satsa? Det kan vara frestande att fördela sina marker mellan enbart händerna 1 och 2. Om någon av dessa vinner, har det lönat sig att inte slösa bort något på hand 3. Men om motståndaren satsar några få marker på hand 3, blir problemet att den fördel man får när hand 1 eller 2 vinner blir mycket mindre än vad man förlorar om hand 3 skulle råka vinna.
Om man spelade ett enormt stort antal händer (och startade med ett bortom astronomiskt antal marker), skulle de optimala satsningarna behöva vara väldigt nära proportionella mot händernas sannolikheter att vinna (med vissa justeringar för möjligheten att flera händer vinner). Men när bara några få givar återstår, kommer det in spelteoretiska aspekter.
För att göra spelet skarpare kan man bestämma att en viss spelare, till exempel A, har vunnit om spelarna har lika många marker kvar på slutet (eller får slut på marker samtidigt). Denna fördel kan balanseras genom att B får starta med något fler marker.
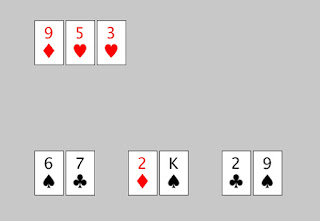
Låt oss säga att det ser ut så här på sista given, och spelarna har en mark var kvar:
Om man tillät oavgjort skulle avslutningen bli ganska slätstruken: Hand 3 har par i nior och kommer att vinna mer än hälften av gångerna. Om jag satsar min mark på hand 3, gör du bäst i att satsa på samma sätt. Den som avviker hamnar alltid i underläge. Men om A kommer att deklareras vinnare vid lika antal marker blir det mer spännande. Spelare B måste då försöka hitta på något annat. Om A satsar på hand 3 medan B väljer att satsa på hand 1 (som får stege både på en åtta och en fyra!), kommer B att vinna mer än var tredje gång.
Fast det är inte så enkelt heller. Om A anar att B tänker satsa på hand 1, kan A korsa B:s planer genom att också satsa på hand 1! Fast B kan förstås då vara en riktig lurifax och i stället själv satsa på hand 3!
Så hur ska man då spela? Svaret är att de optimala strategierna är randomiserade. För att inte bli lurad ska du i princip ha en personlig och hemlig slumptalsgenerator som i viss mån styr ditt spel. I det här fallet vinner den första handen 323 gånger och den tredje handen 487 gånger, av 903. Hand 2 vinner 93 gånger, vilket är för lite för att det ska vara rätt att någonsin satsa på den. Med bara två alternativ är regeln att spelare A, som har fördel, ska göra fel på hand 1 och hand 3 lika ofta åt båda hållen, medan spelare B som är underdog ska gissa rätt lika ofta på hand 1 som på hand 3. A ska alltså betta på hand 1 med sannolikhet $323/(323+487)$ och på hand 3 med sannolikhet $487/(323+487)$, och för B blir det tvärtom. Spelare B vinner med sannolikhet \[\frac{323\cdot 487}{(323+487) \cdot 903},\] eller ungefär 21.5%, och A alltså med sannolikhet 78.5%.
Mer komplicerat blir det om spelarna har flera marker kvar och alla tre händerna är aktuella att satsa på. Men det får räcka med spelteori för den här gången!
